小学5年生 算数<11月>台形の面積/いろいろな図形の面積割合・百分率の意味と求め方 練習問題プリント 台形の面積、文章題、色々の図形の面積、文章題、割合・百分率、文章題面積シートで三角形及び円弧・正六角形を計算して、確認の為に作図ソフト (エクセル)を付加したものです。 (印刷倍率はほぼ11で合わせてあります。 ) 1度作図して数値を変更しても追従します又ワンタッチ釦 (紫色釦)でも可能ですので確認してみて下さいね。 表計算は (1)3辺が与えられた時 (ヘロンの公式) (2)2辺と挟む角度が90度の時 (3)フィレット部外の面積さらに,一定の面積となる長方形や正方形を作らせたり,複合図形の面積を求めさせたりするなどの,作 業的・体験的活動を積極的に取り入れるようにして,面積についての量感を豊かにする指導を工夫していき たい。 (4) 算数的活動について 「1c㎡,1㎡等を単位とした面積を敷き詰める」と

平面図形の苦手を解消 三角形の面積比 基本編
図形の面積 積分
図形の面積 積分- つまり,上半分の長方形の面積をたて×よこで計算してから, おうぎ形(灰色) の面積を計算して,引き算をすれば, 黄色の図形 の面積を求めることができるのです。 それぞれの面積を計算する前に,長さのわかる辺は長さを記入していまいましょう。314×64=096 314×81= 正方形や円などの面積を速く正確に計算するために、同じ数をかけた積(二乗・自乗)の計算方法をマスターしましょう。 (参考) → 二乗の速算法 平面図形の面積の基本問題 問題1 次の図形の黒くぬった部分の面積を求めなさい。 → 解答




いろいろな面積を求める問題1 中学受験準備のための学習ドリル
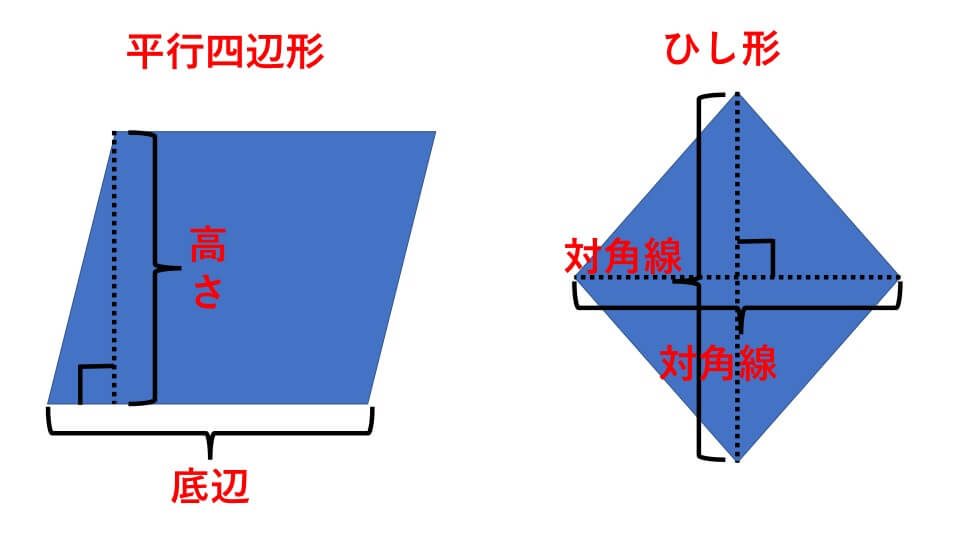
クイズ442図形の面積を求める () クイズ353図形の分割 () クイズ円玉で逆三角形を作る(図の問題) () クイズ196図形を二等分せよ () クイズ186ブロックで埋める方法 テトリスパズル () クイズ1二つの正方形の大きさは (どんな図形の面積も,三角形を基にし て考えると求めることができますね。単 位に注意して計算してくださいね。 (三角形) (台形) (ひし形) A B 底辺 C 高 さ 底辺 高 さ 底辺 高 さ (平行四辺形) 小学★ 5年 5①C P1 学習日 年 月 日 単 元 年 組 番 8問 5年「面積」 氏名 1 次の図形の面積を④ 面積と比例の関係 教え方1 平行四辺形の面積の求め方 その前に4年の面積の求め方の勉強を思いたださせたいと思います。 下の複合図形の面積を求めるには、長方形や正方形の形におきかえて面積を求めたことをふりかえらせて下さい。
⑵ 図形の面積を求める活動や求めた結果を発表する活動など,一単位時間のねらいをしぼり,そ のねらいに応じた算数的活動を展開上に位置付け,効果的に学習ができるようにする。 ⑶ 長方形の面積を求める公式「たて× すると図形は、たて(402)cm、横(302)cmの長方形になるので、面積は、 (402)×(302)=1064 よって、 答え 1064㎠ 面積③ 円が絡んだ複雑な図形 例題3 下の図の色の付いた部分の面積を求めなさい。ただし円周率は314する。 解説 下の図のように図形を分けて、考えます。A = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径
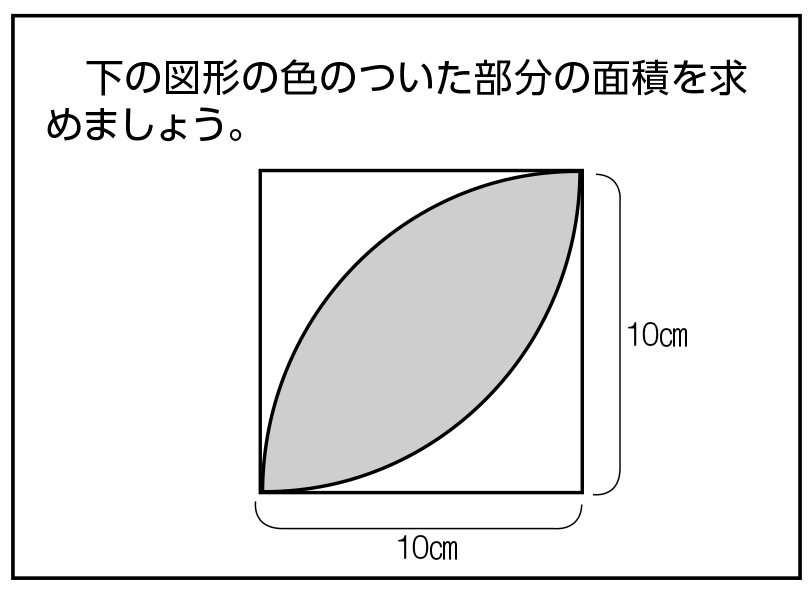
三角形の面積 ・正三角形の面積 1辺の長さを指定して、正三角形の面積を計算します。 ・三角形の面積(底辺と高さ) 底辺と高さから三角形の面積を計算します。 ・三角形の面積(2辺と間の角度) 2辺と間の角度から三角形の面積を計算します。図形の面積に関心をもち,図形を分解したり合成したりする具体的な操作を通して,基本的な面 積の求め方を調べようとすることができる。 (学びに向かう力,人間性等) 4 単元計画(12時間) 段 階 配 時 主な学習活動・内容 指導上の留意点 評価規準 (評価方法) 導 入 1 1まず、全体の面積を求めて、その半分の面積の図形を作ればいいことに気付かせるようにする。 長方形・三角形・台形などの図形を考えることで半分の面積に分けることができることに気付かせる。 3 問題を把握し、今日の課題を知る。 半分に分ける図形が10cmの辺を生かして考える場合
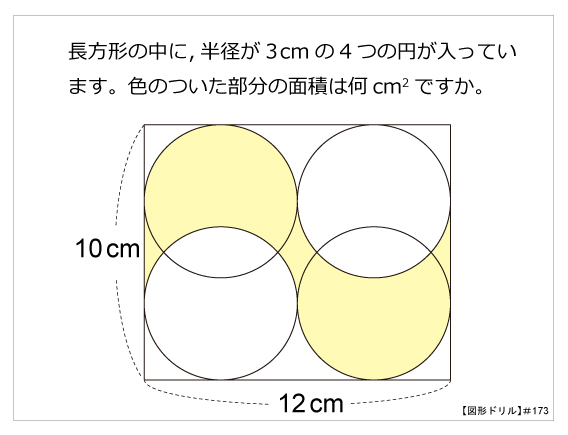



図形ドリル 第173問 複合図形の面積 算数星人のweb問題集 中学受験算数の問題に挑戦
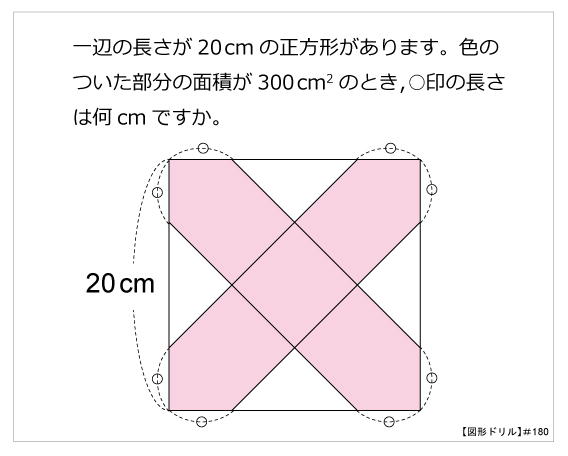



図形ドリル 第180問 バツ型の面積 算数星人のweb問題集 中学受験算数の問題に挑戦
複合図形の面積の求め方を考えることを通してその図形が長方形を組み合わせた図形である ことに気付き,求積に必要な条件を見いだすことができる。 思考・判断・表現 (2) 準備 複合図形の提示物,ものさし,ワークシート (児童用) (3) 展開 学習活動・内容 教師の支援と評価基準 周の長さが一定である図形の中で,面積が最大のものは円です。 (等周定理) 等周定理の厳密な証明は少し大変なので,ここでは等周定理に関連して 「対称性が高い図形は面積が大きい」 というテーマで,高校数学で分かる性質をいくつか紹介します。 → 等周問題に関連する高校数学の問「図形電卓 ShapeInfo」のレビューをチェック、カスタマー評価を比較、スクリーンショットと詳細情報を確認することができます。「図形電卓 ShapeInfo」をダウンロードしてiPhone、iPad、iPod touchでお楽しみください。




面積の求め方 算数の教え上手 学びの場 Com
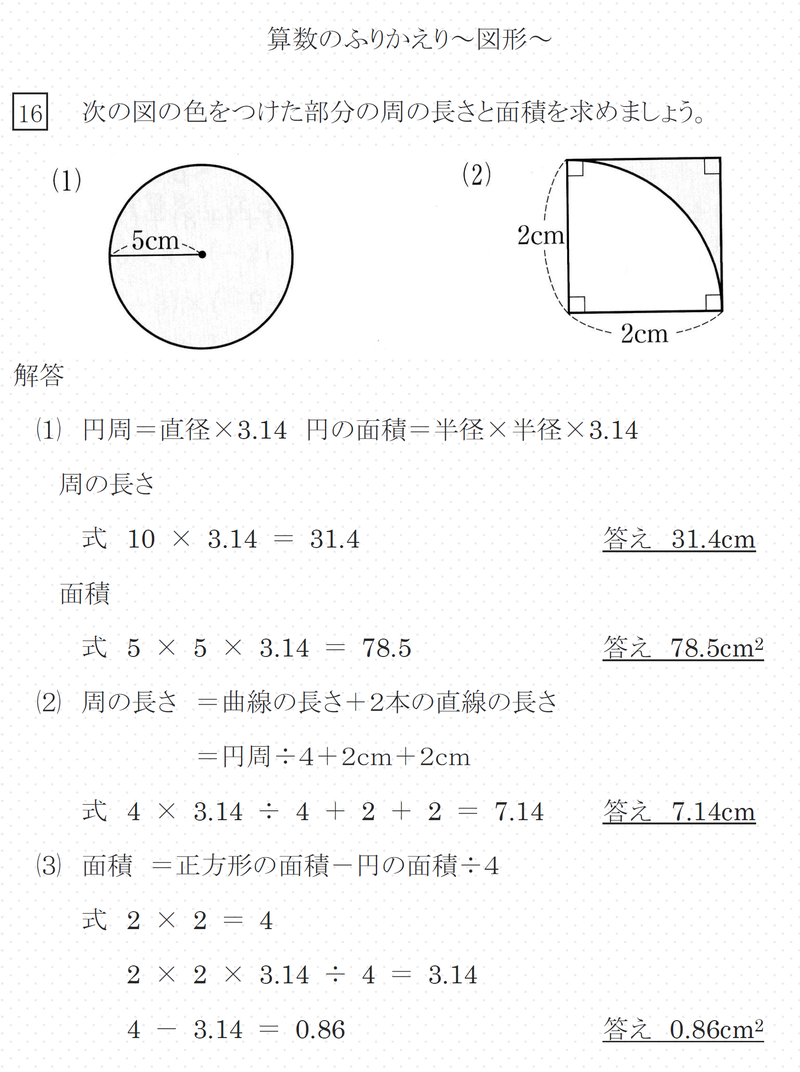



小学6年生 算数 図形の面積や体積 赤城 ᐡᐤᐡ
右図1のような三角形の面積は、いずれも (底辺)×(高さ)÷2 で求められます。 次のように分数の形で書くこともできます。 (面積)= (1) 2で割ることを忘れる答案が多いので注意しましょう。 右図2の三角形の面積は、 4 × 3=12 ではなく、 4 × 3 ÷ 2=6 になります。 (2) 高さは必ず底辺に垂直三角形 (さんかくけい) の 面積 (めんせき) の求め方の 基本 (きほん) は「 底辺 (ていへん) × 高 (たか) さ ÷ 2」ですが、高さが分からないときに 他 (た) の 情報 (じょうほう) から面積を求める 公式 (こうしき) がいくつもあります。Hello School 算数 体積・表面積 インターネット上で受験算数の一通りの基本的解法をマスターしよう♪。



座標と図形の面積 中学から数学だいすき




難関校頻出 複雑な平面図形の面積を求めるには
図形の面積の求め方のテクニック「1 分割する」 問題)上の図の四角形abcdの面積は何c㎡ですか? 四角形を三角形二つに分割して解きます。 三角形abdと三角形bcdになりますので、 =6+5 =11c㎡ 図形の面積の求め方のテクニック「2 余分なところを引く」以上の区別が付けられるようになればOKです! 終わりです~。 図形のこと ベクトル 中3数学 図形の性質 よかったらシェアしてね! URL Copied!台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から) 円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から)
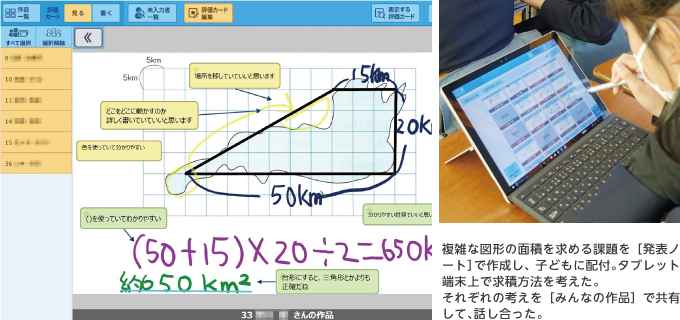



茨城大学教育学部附属小学校 学校とict sky株式会社 Ictを活用した学習活動をサポート



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生
正方形の面積 長方形の面積 台形の面積 台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から) 円に内接する四角形の面積(4辺から)1辺の長さがa (cm)の正方形ABCDがあるとき,Bを中心とする半径a (cm)の円とDを中心とする半径a (cm)の円の共通部分の面積 (cm 2) ヒント 3 次の図のように半径10 (cm)の円の中に半径5 (cm)の円が2つ接しているとき,斜線部の面積 (cm 2) ヒント 図のように小さい円の半分を回転させると,凸の部分がちょうど凹の部分に重なるから,大きい円の面積の半分を求めるとよい (む空間図形 相似な立体では 長さの比は相似比と同じ。 面積比は相似比の2乗。 体積比は相似比の3乗。 相似比がabの相似な図形の場合 辺、高さなど 長さの比は a b 表面積など 面積比は a2 b2 体積



図形の扉 面積って何



1
平面図形の面積比 右の図のように、相似比が m n である2つの三角形の面積比 S S ′ を考えてみよう。 相似比が m n であるから、底辺の比は m n 、高さの比も m n となるので、左側の三角形の底辺と高さをそれぞれ a 、 h とすると、左の図の右側 の三角形の底辺と高さは a × n m 、 h × n m となる。 これより、 S S ′ は S S ′1図形の基本単位は三角形 2四角形は三角形に分割する 3補助線は1本引いただけで考えてみる 4候補の数だけ図を書いてみる 5高さの等しい三角形の面積比=底辺の比 という、5つの大切なポイントが復習できます。 「平面図形と比」の問題が苦手という 57cm²という結果は、正方形の面積100cm²の57%にあたります(正方形の面積の057倍)。 つまり、葉っぱ型の図形の面積は (1辺の長さ)×(1辺の長さ)×057 でもとめることができるのです。 この公式を覚えておくと、問題を効率よく解くことができます。




平面図形の苦手を解消 三角形の面積比 基本編




中央線を使った図形の面積 スクールプレゼンター教材共有サイト スクプレ道場
面積を求めよう 1 (平行四辺形や三角形の面積) 面積を求めよう 2 (平行四辺形や三角形の面積) タイルの色ぬり (平行四辺形や三角形の面積)おうぎ形 (半径と中心角から弧や面積を出す) おうぎ形 (半径と弧または面積から中心角を出す) おうぎ形 (半径を求める) おうぎ形 (総合) 平面図形面積 (発展) ① 70cm 2 ② 9πcm 2 ③ 56cm 2 ④ 11πcm 2 ⑤ (25π50)cm 2 ① 47 2 πcm 2 ② 33 5 πcm 2 ③ (8π16)cm 2 (1) 15πcm 2 (2) 216° (1) 6πcm (2) 135° (1) 18cm (2) 50° 全体の図形の面積の 何分のいくつでしょうか? 」 という問題を解くコツについて、 お話をしていきます。 今回のお話は 三角形の面積比を使用しますが、 三角形の面積比の求め方には 高さが同じ三角形の場合や




直方体を切り取った図形の面積 数学i By Okボーイ マナペディア
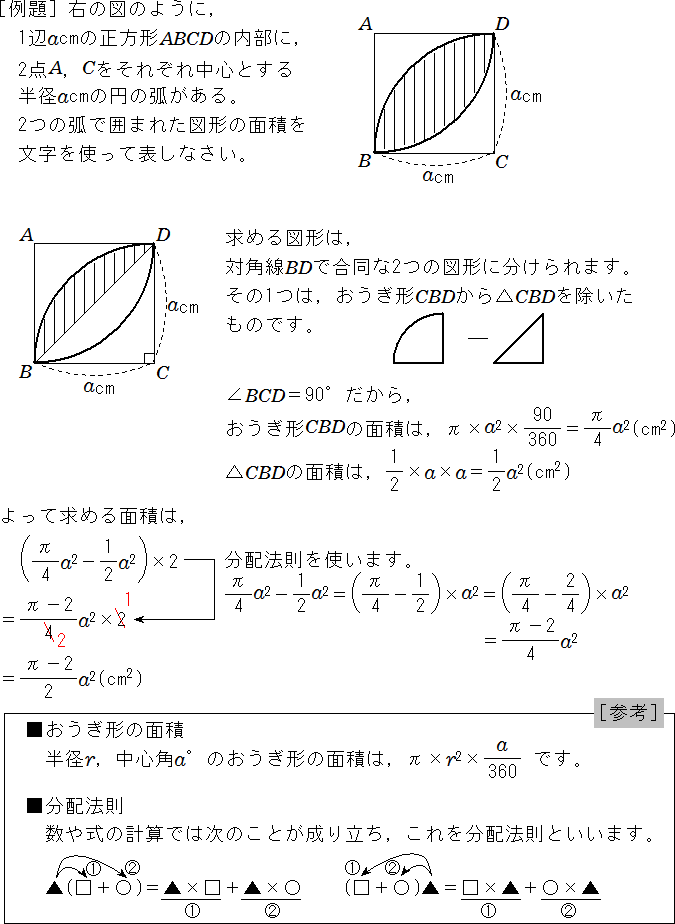



式の計算 文字を使った変わった図形の面積の求め方 中学数学 定期テスト対策サイト
定義 平面図形については、2次元空間内の部分集合(つまり図形)の定義関数を積分して面積を定義する。 直感的にはまず長方形の面積を定義し、一般の図形に対しては小さな長方形の集まりでその図形を近似した極限を以って面積を定義する。 曲面については、定義関数の面積分のほか3.複合図形の面積を調べる。 個人解決の様子 発表の準備 ・図に言葉や記号等を記入させ,筋道を立てた説明ができるようにさせる。 ・全体から部分を引く方法のヒントカードを用意し,その方法で解決させる。 4.全体で話し合う。 (児童による3つの方法の発表の後) ・この方法




小学5年生 算数 11月 台形の面積 いろいろな図形の面積 割合 百分率の意味と求め方 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ



2



中学受験 算数 面積 よく出る応用問題や難問をわかりやすく解説 中学受験アンサー
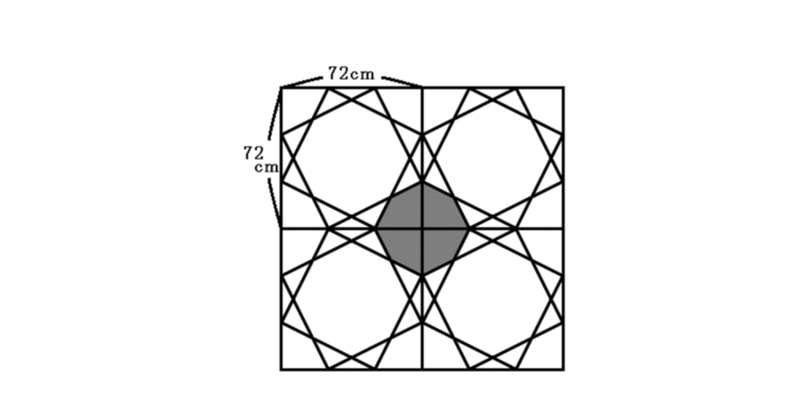



徳島県立 共通 18算数 図形の面積 中高一貫 適性検査解説 Note




小学5年生 算数 11月 台形の面積 いろいろな図形の面積 割合 百分率の意味と求め方 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ
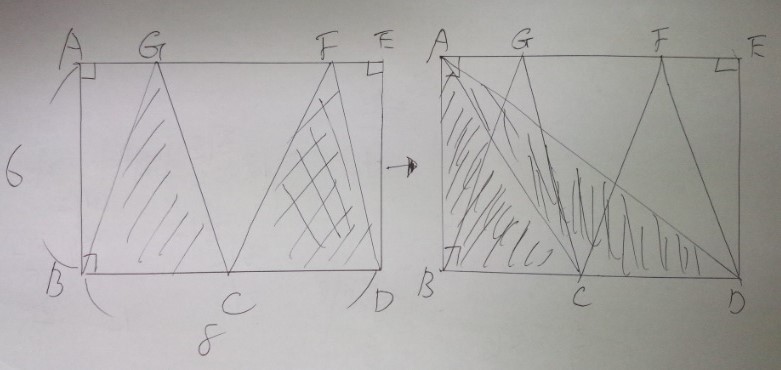



図形の面積の求め方のテクニック 基本編 中学受験 塾なし
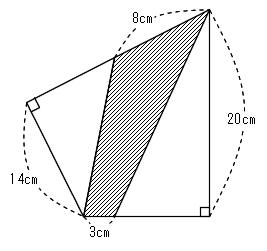



図形の面積問題を得意にする6つのチェック 効果的な勉強方法は 前田昌宏の中学受験が楽しくなる算数塾




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ



小学生の算数 図形 面積 体積 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 小学生




平面図形と面積 比を究める15題 Myisbn デザインエッグ社 清水良太郎 本 通販 Amazon
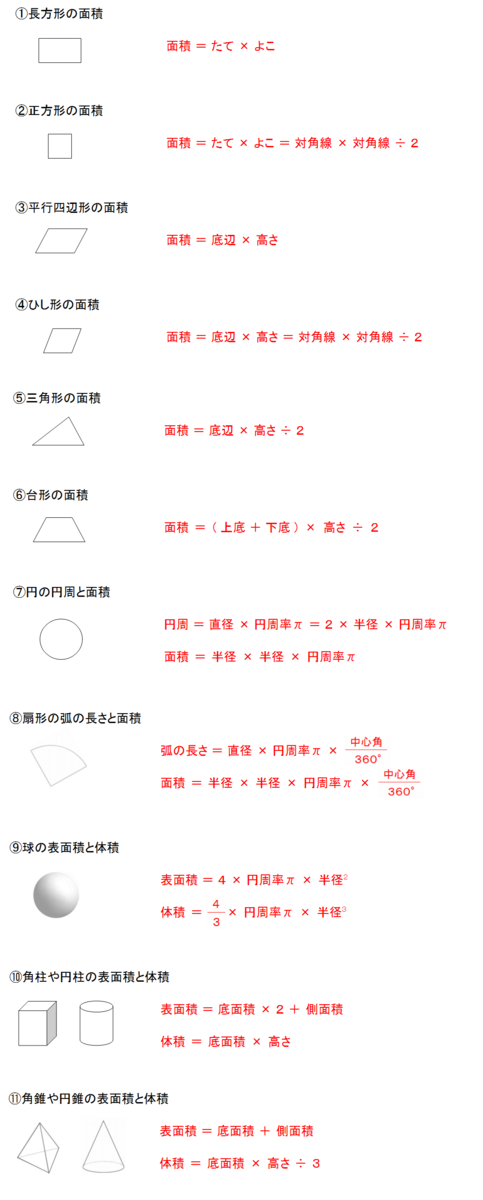



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師




この図形の面積の求め方を教えてください お願いします この図形 小学校 教えて Goo
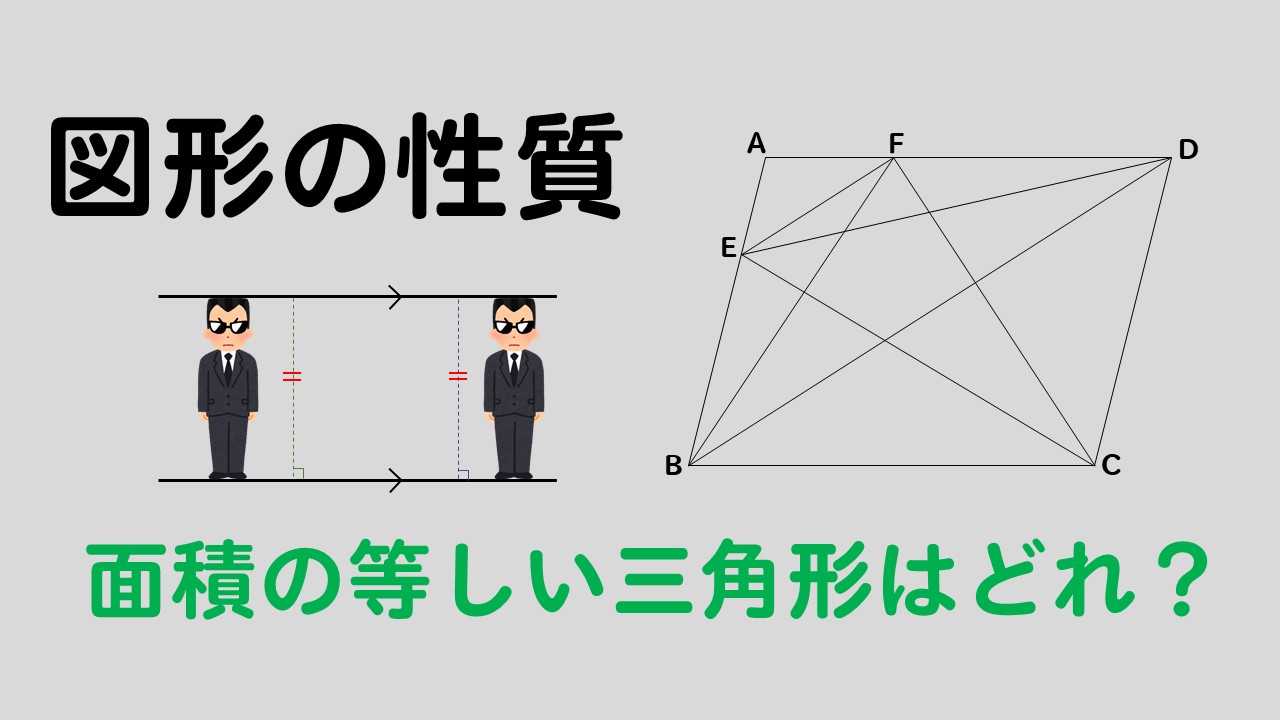



中2数学 平行四辺形の中から面積の等しい三角形を見つける問題を解説 数スタ




Telecharger 面積計算アプリ 図形計算 Pour Iphone Sur L App Store Education




円の面積の求め方を一通り身につけたら 少し応用的な問題にも挑戦してみましょう 円の面積の応用問題をやってみよう 円の面積の もっと基本的な問題のノート例はこちらです 円の面積 数学ノート 学習ノート 学習
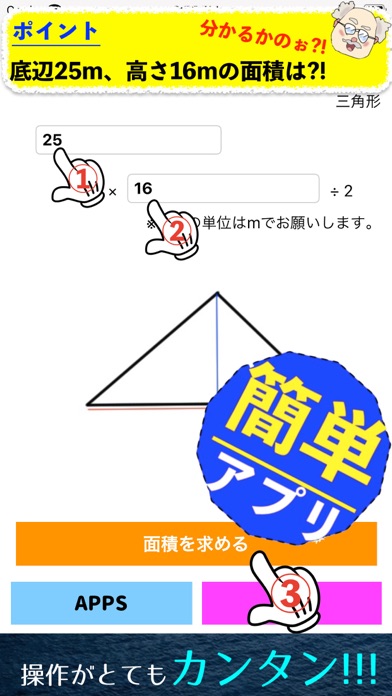



Telecharger 面積計算アプリ 図形計算 Pour Iphone Sur L App Store Education




図形の面積 情報過多 スクールプレゼンター教材共有サイト スクプレ道場



小6算数 円の面積 指導アイデア 2 みんなの教育技術




標準 おうぎ形と正方形の面積 なかけんの数学ノート
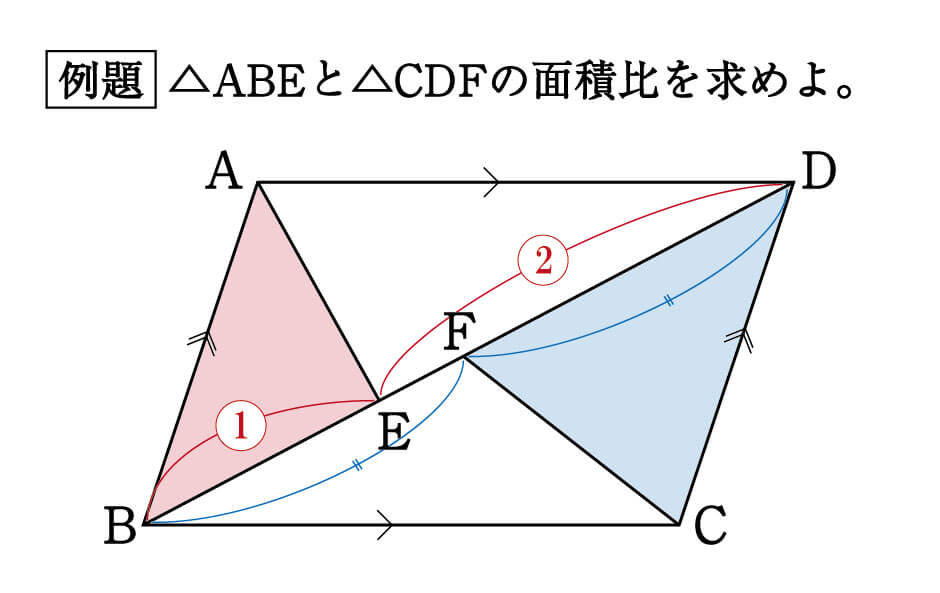



数学 なぜ面積比は苦手になりがちなの 面積比 集中特訓 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




図形の面積比 体積比 数学i フリー教材開発コミュニティ Ftext




写真のような図形の面積の求め方で 四角形から引くやり方以外で解き方はありますか Clear
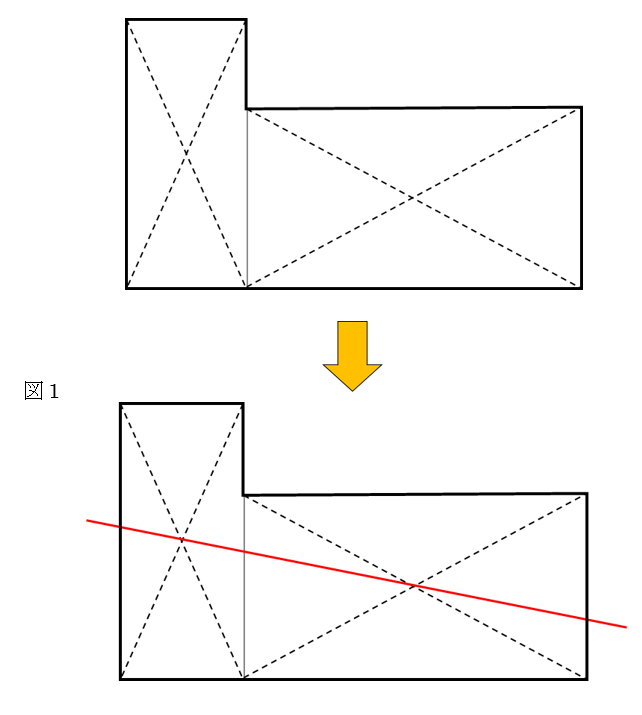



面積を2等分する考え方 中学受験プロ講師ブログ
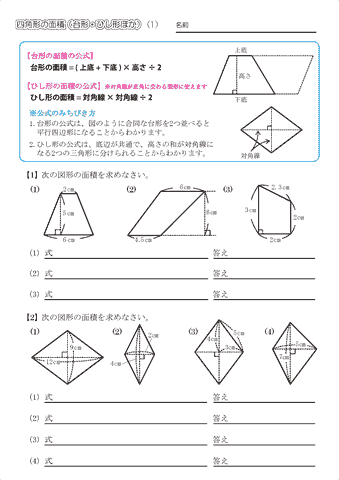



小学5年生の算数 四角形の面積 台形 ひし形ほか 問題プリント ちびむすドリル 小学生



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生




いろいろな面積を求める問題1 中学受験準備のための学習ドリル



2
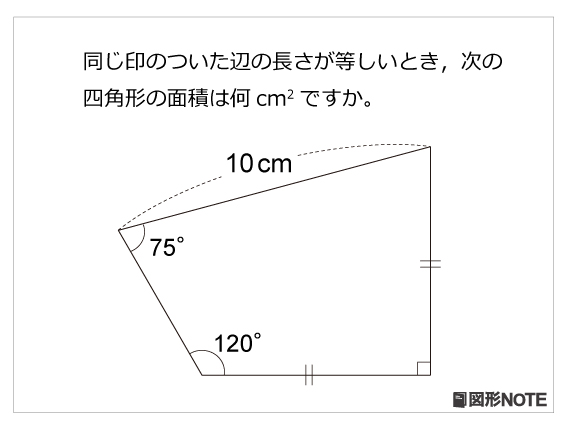



図形noteプレ レベル5 複合図形の面積 算数星人のweb問題集 中学受験算数の問題に挑戦




小5算数 図形の面積 指導アイデア みんなの教育技術
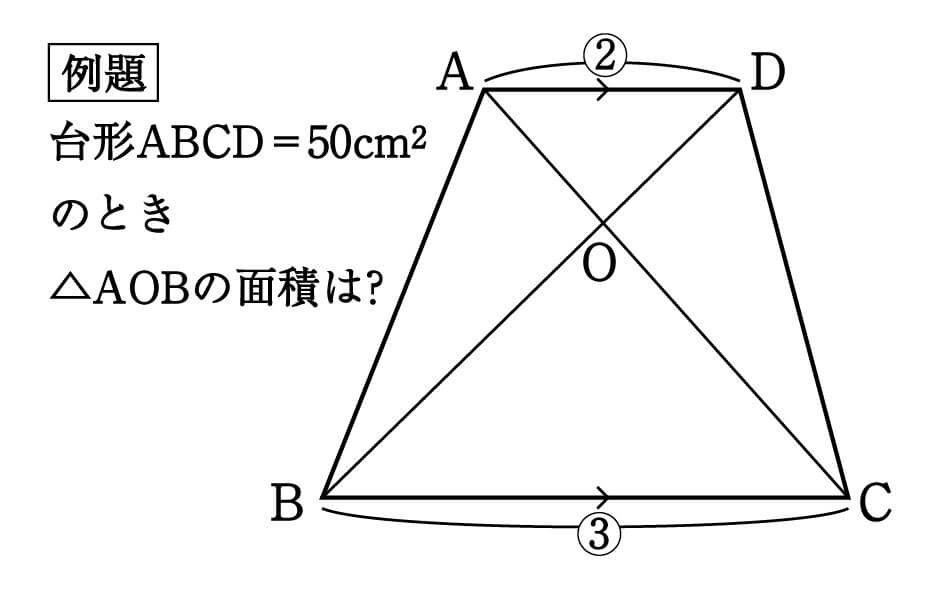



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
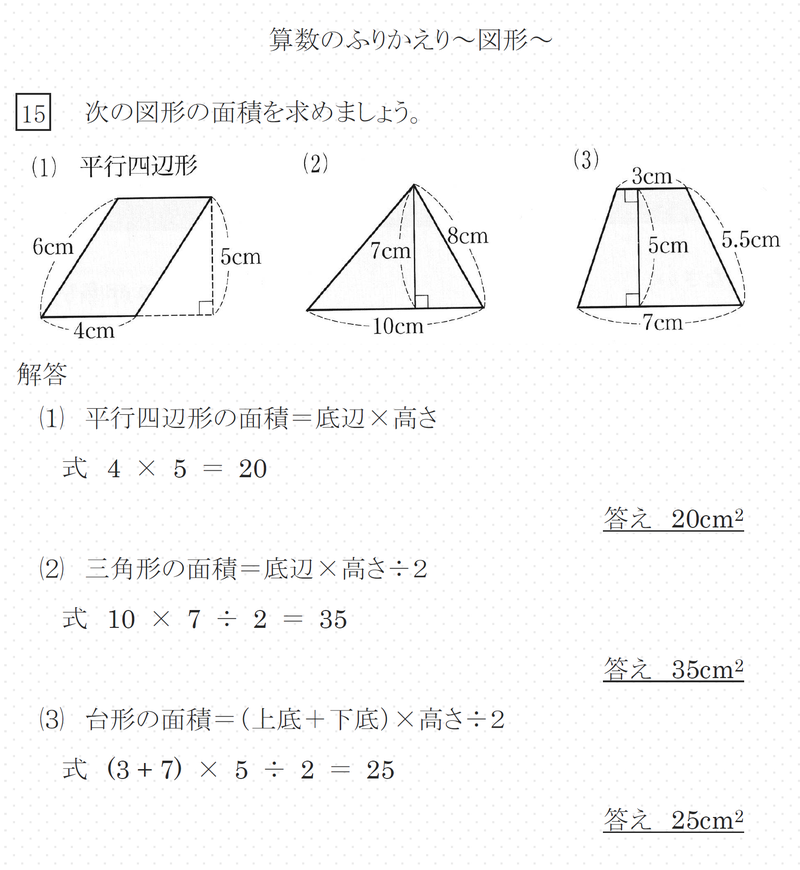



小学6年生 算数 図形の面積や体積 赤城 ᐡᐤᐡ



教育ソフト開発研究所 5年5巻




難関校頻出 複雑な平面図形の面積を求めるには




面積が変わる不思議な図形 この謎が解けますか 数学の面白いこと 役に立つことをまとめたサイト




相似な図形の面積比の問題 相似比を出してから二乗しよう 中学や高校の数学の計算問題




図形の面積比 知っている人は5秒以内には解ける面積比の裏技 Youtube




Python 図形の面積 体積を計算してみよう プログラミングで数学 くれあブログ




5年算数 図形の面積ふりかえり Ict教育推進研究所の資料室




中学数学 相似な図形の面積比 中学数学の無料オンライン学習サイトchu Su




この図形の面積の求め方を教えてくださいm M Clear



図形 面積比の応用 三角形の面積比 名古屋市北区の学習塾は思考力を育む 泰成スクール




平面図形の面積の求め方 基本編 中学受験 塾なし の



中学受験 図形の面積問題は 7つ道具 で攻略 かるび勉強部屋
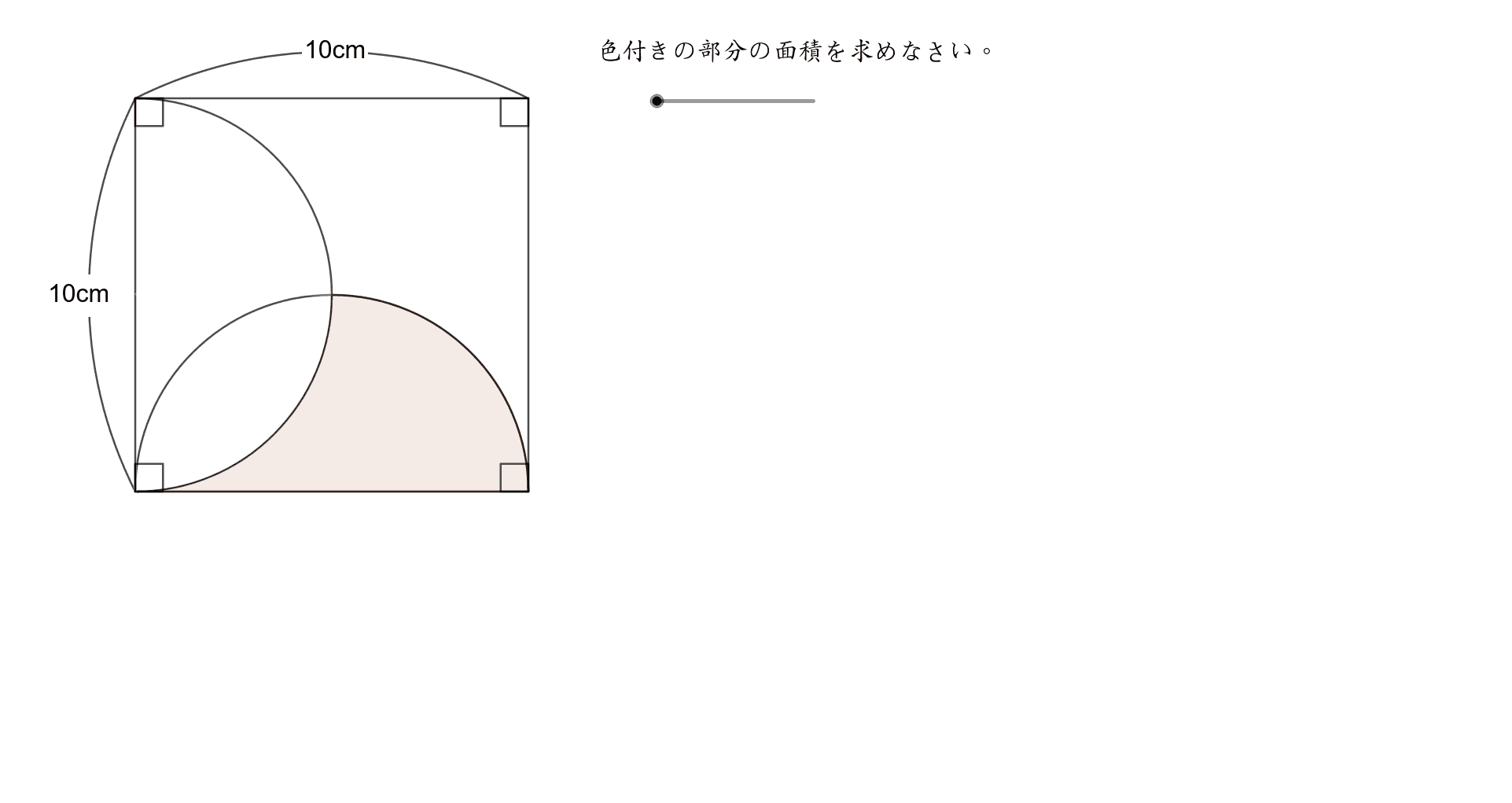



複雑な図形の面積 Geogebra




5年生で 様々な図形の面積の求め方を習いますが ここでは 平行四辺形と三角形の面積の求め方を学習する自主学習ノートの例を紹介します 平行四辺形と三角形の面積を求める 三角形の面積 学習 学習ノート 子どもたちの研究
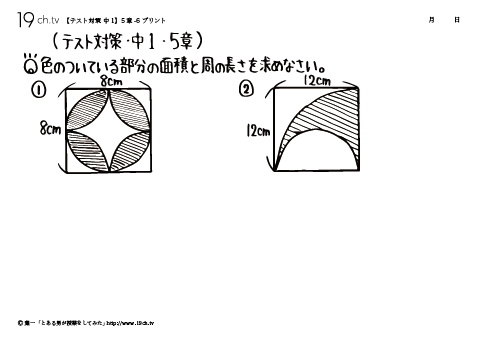



複雑な図形の面積 19ch




算数 扇形の面積の応用 葉っぱ型図形の面積 なるほどの素




平面図形の面積 まとめ7 8 いろいろな図形の面積 Youtube
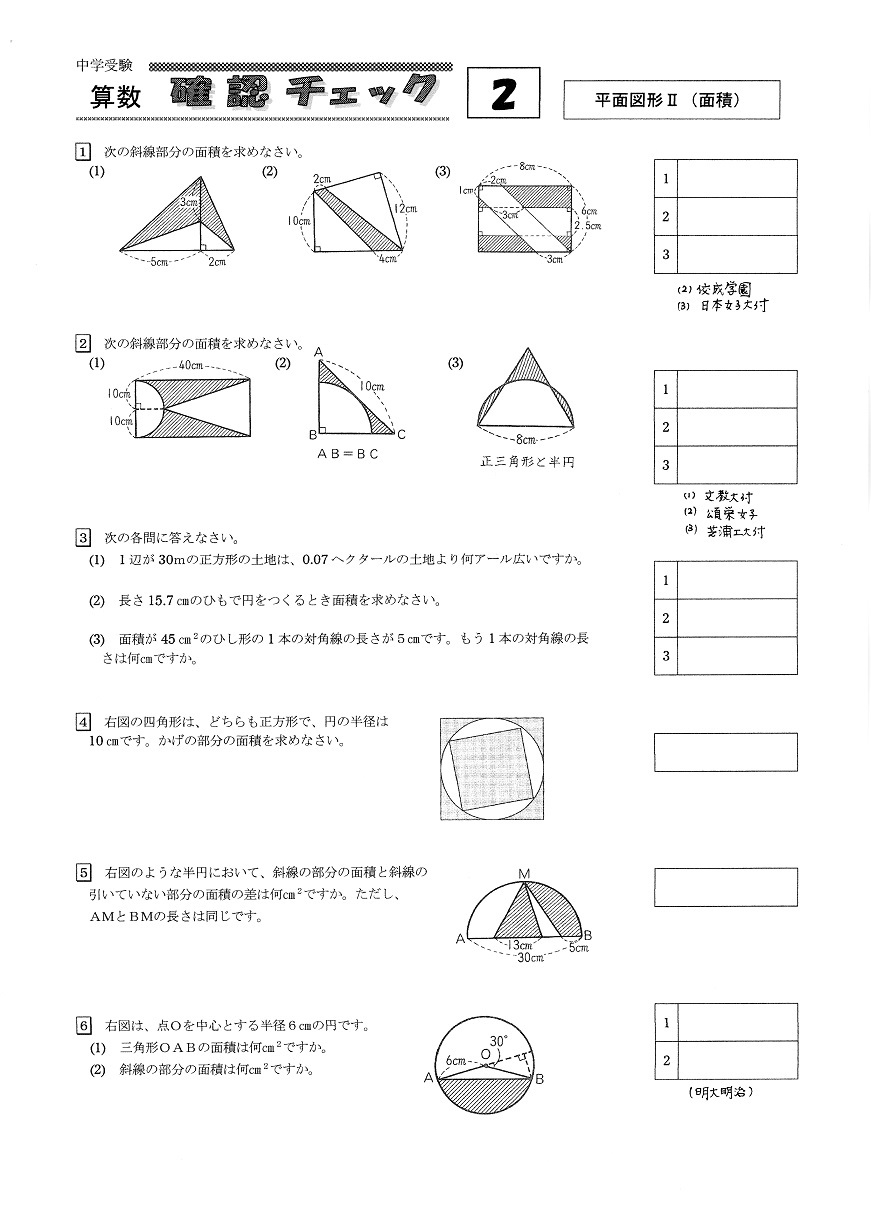



中学受験 算数確認チェック2 平面図形 面積 グランパは元塾長




土地を等しく分割せよ 図形の面積 さんすう刑事ゼロ Nhk For School




中学受験 算数 面積 よく出る応用問題や難問をわかりやすく解説 中学受験アンサー



面積 これが中学入試に出た図形問題
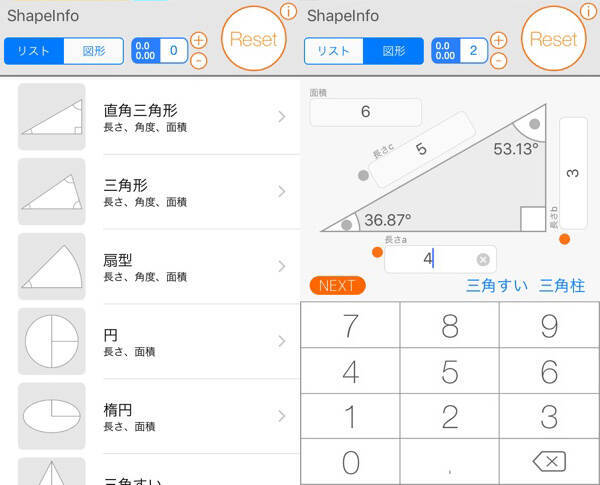



三角形や球も 様々な図形の面積や角度がすぐに分かる 図形電卓 が超便利 16年2月5日 エキサイトニュース
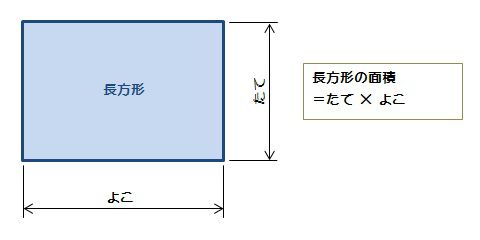



長方形の面積 算数の公式覚えてますか




はっぱ型 の図形の面積 身勝手な主張
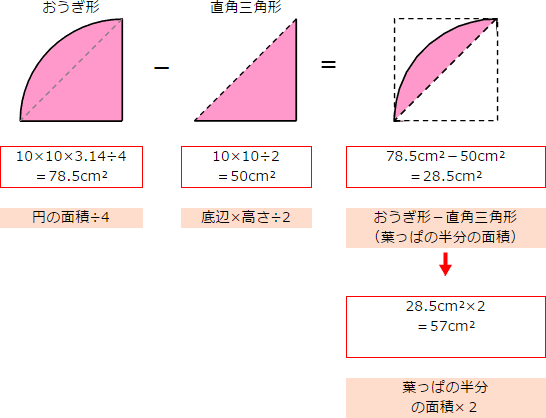



面積の求め方 算数の教え上手 学びの場 Com
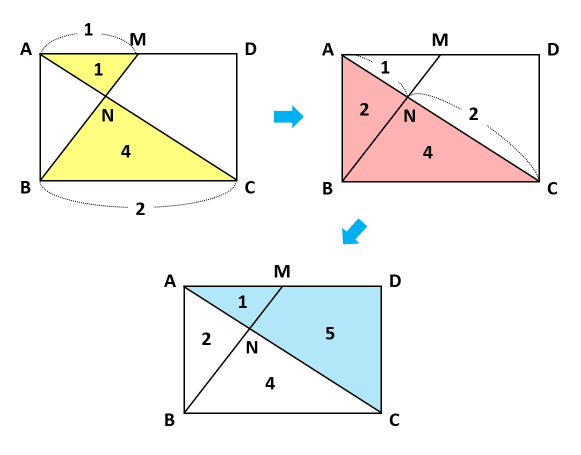



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ
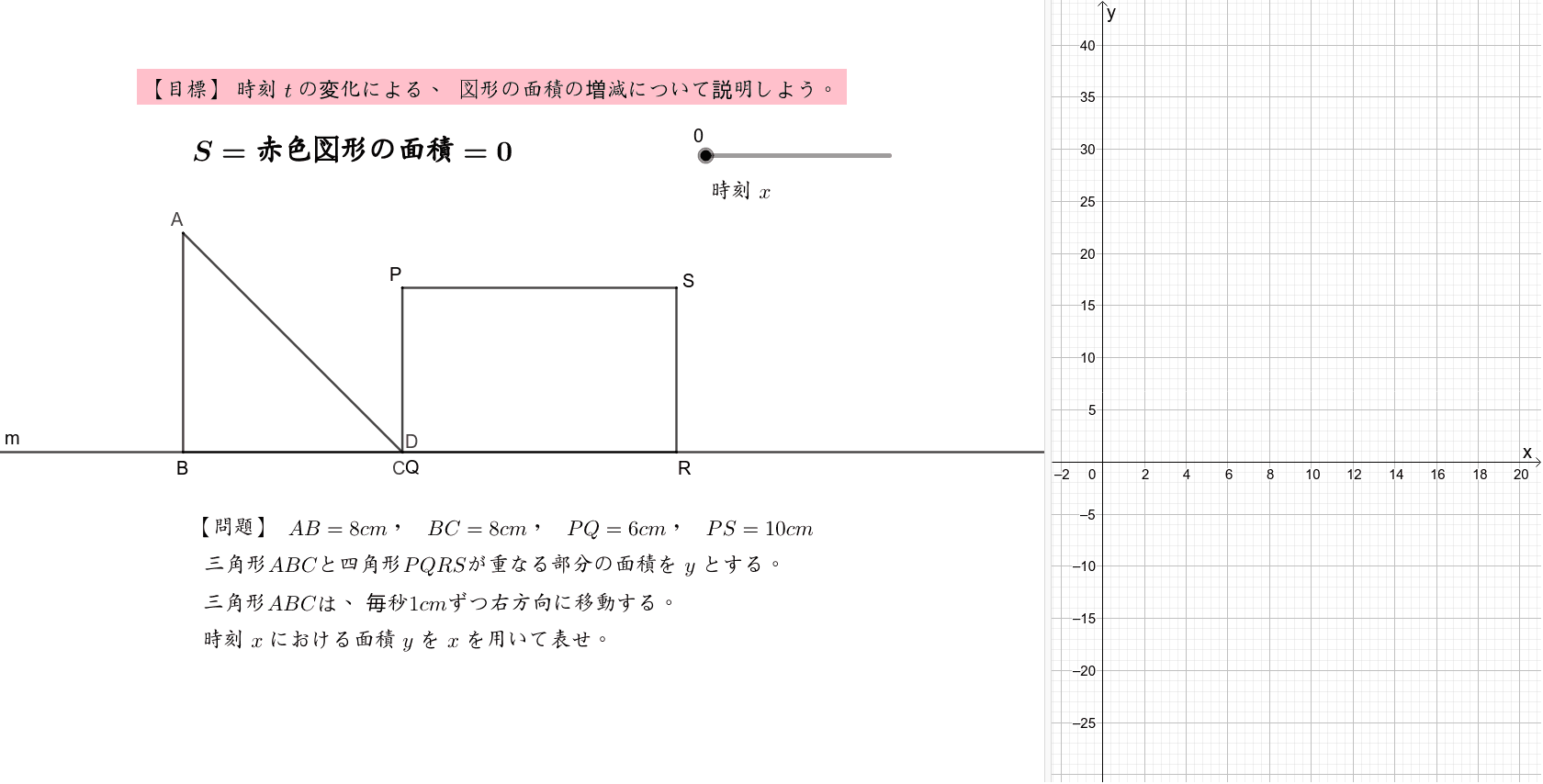



動点と図形の面積2 Geogebra




複雑な図形の面積を求める際に計算方法をどうすべきか 式をバラさずに書くことの大切さ 墨田区両国のプロ家庭教師みみずく 総武線 大江戸線 新宿線沿線で指導中
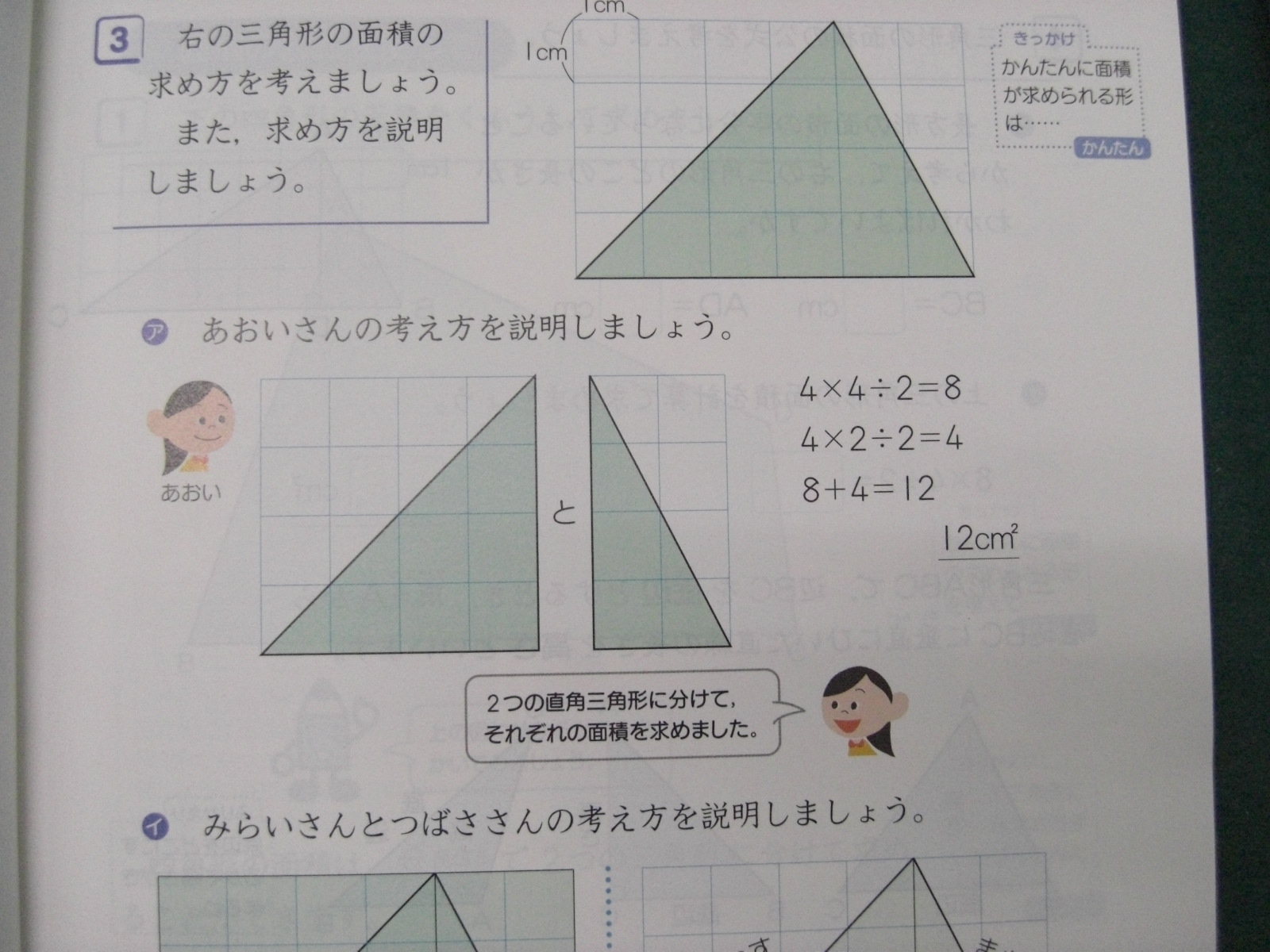



図形の面積 石原清貴の算数教育ブログ



図形の面積 算数 指導案 算数5年生の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材



3
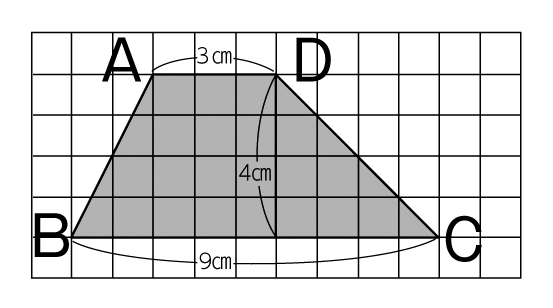



小5算数 図形の面積 指導アイデア みんなの教育技術




ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun




5年算数面積 教え方のポイント




三角形の面積の公式 小学生に教えるための分かりやすい解説 数学fun



250枚 至急 葉っぱ形の図形の面積について質問です Yahoo 知恵袋




図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト



1




面積問題 小学4から6年生 算数問題プリント




空間図形に含まれる三角形の面積を求める問題 直方体 数学i By ふぇるまー マナペディア




高校数学 放物線と直線で囲まれる図形の面積 映像授業のtry It トライイット



1




いっきに極める算数小学3 6年の図形と面積 体積 本 通販 Amazon




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
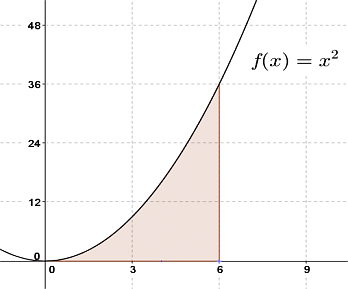



積分 積分スゴい 曲線図形の面積を求めてみよう 大人が学び直す数学




相似な図形の面積と体積 の勉強法のわからないを5分で解決 映像授業のtry It トライイット




高校数学b 三角形の面積のベクトル表示 成分表示とその証明 受験の月
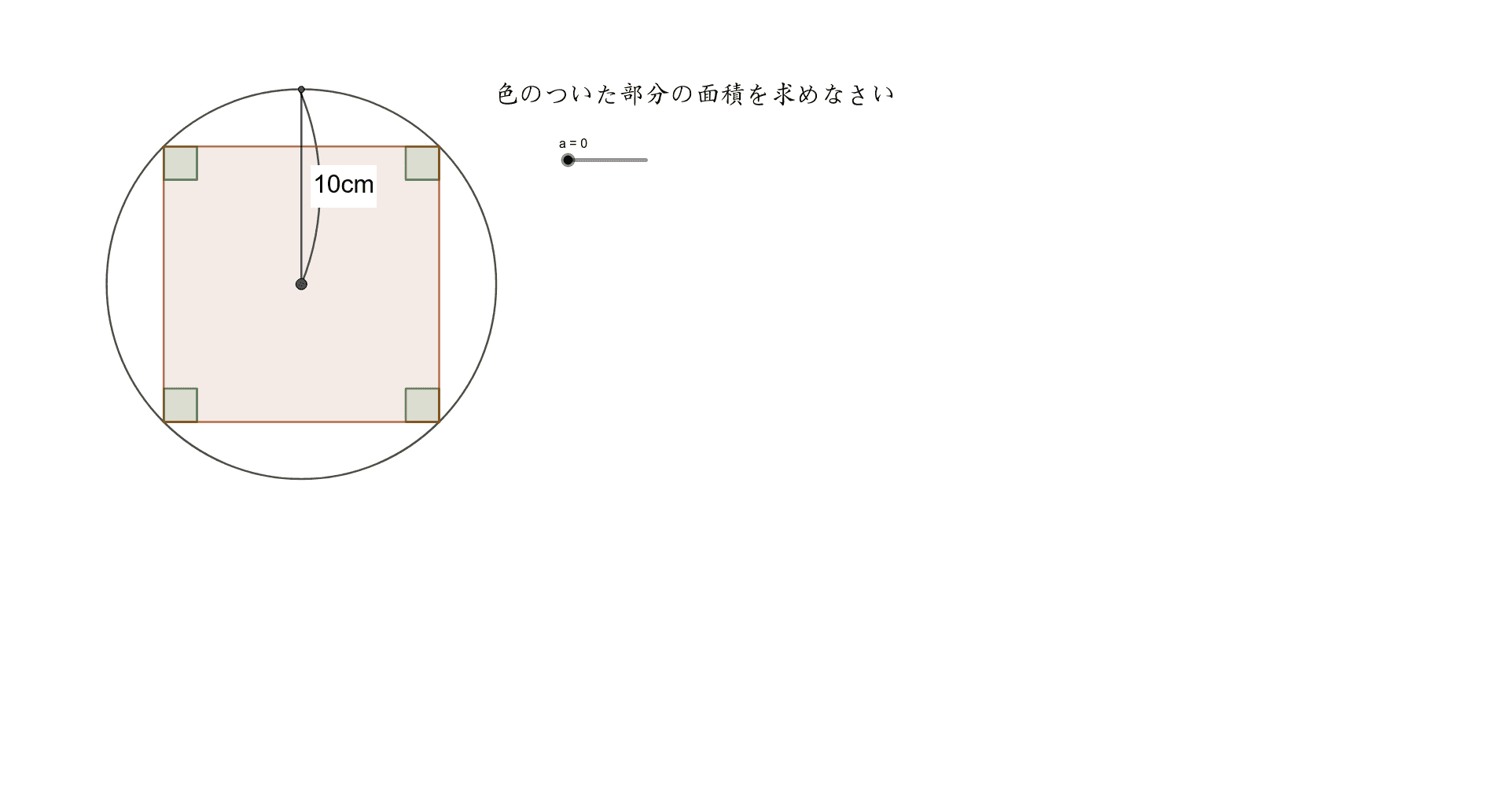



複雑な図形の面積 Geogebra
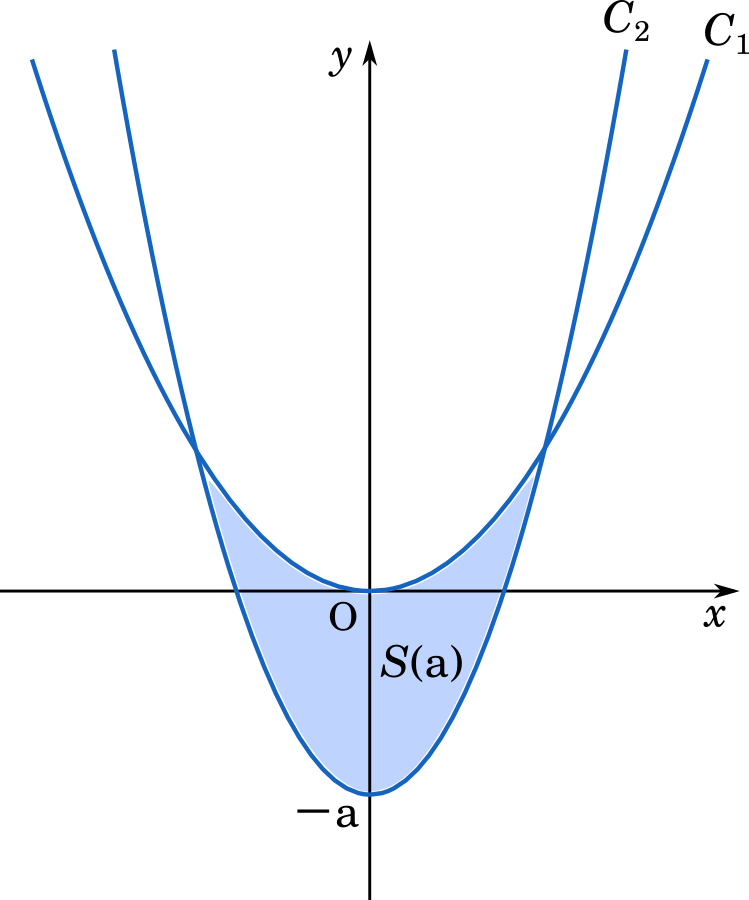



東京都立大18理系第1問 2 つの二次関数で囲まれた図形の面積の求め方 最小値を微分で求める Mm参考書
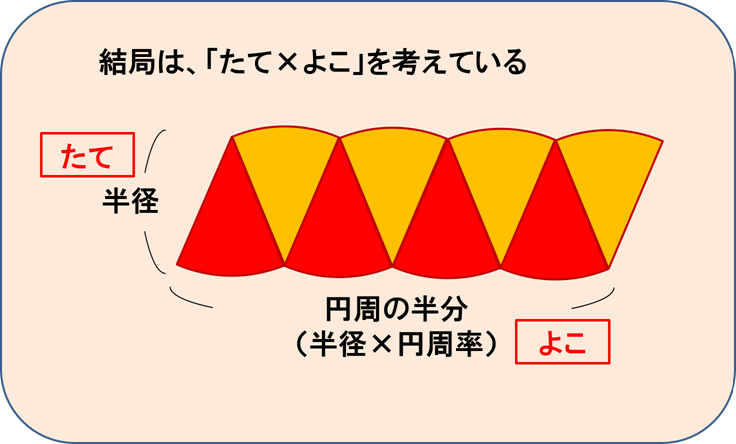



中学受験算数 平面図形 面積比の基本 中学受験プロ講師ブログ




算数 図形の面積2 平行四辺形 授業力アップ 学級経営の話




円の面積 練習応用 Youtube
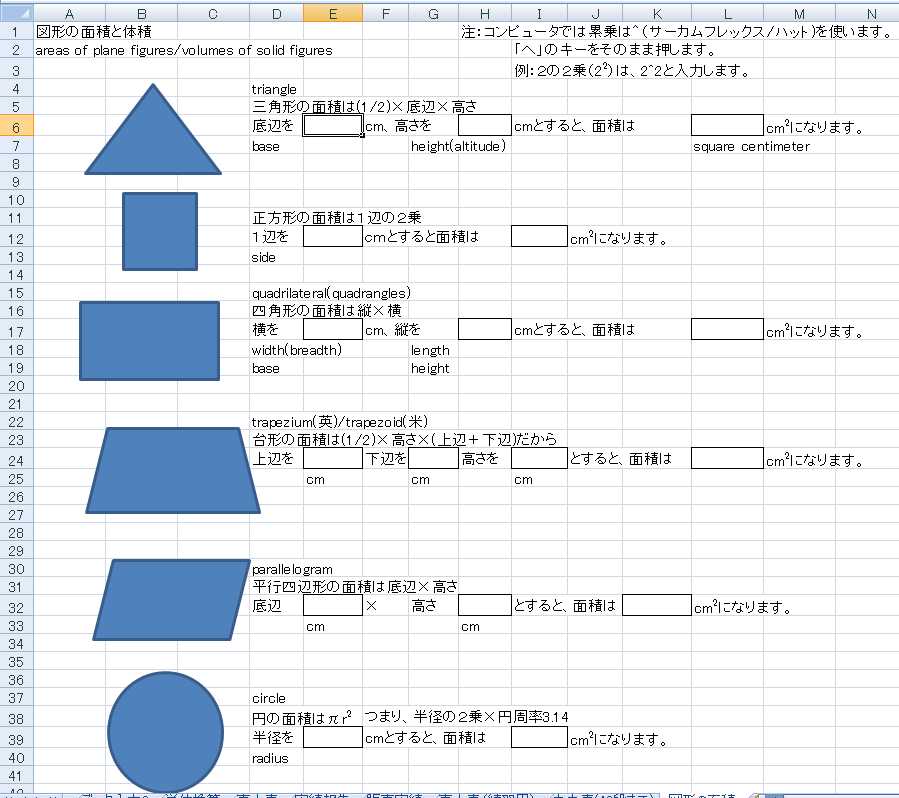



図形の面積と体積 しるぼの独り言




4つの乗法公式を図形の面積を求めることと考えてみよう 中3向けの動画です Studychannel スタディチャンネル 勉強が楽しくなる 学び 動画サービス



算数合格力をつける基礎1000本ノック 直線図形の面積 Senbon Knock Set Chokusenzukeimenseki 数理教育研究会yahoo 店 通販 Yahoo ショッピング




すきるまドリル 小学5年生 算数 図形の面積 無料学習プリント すきるまドリル 無料学習プリント
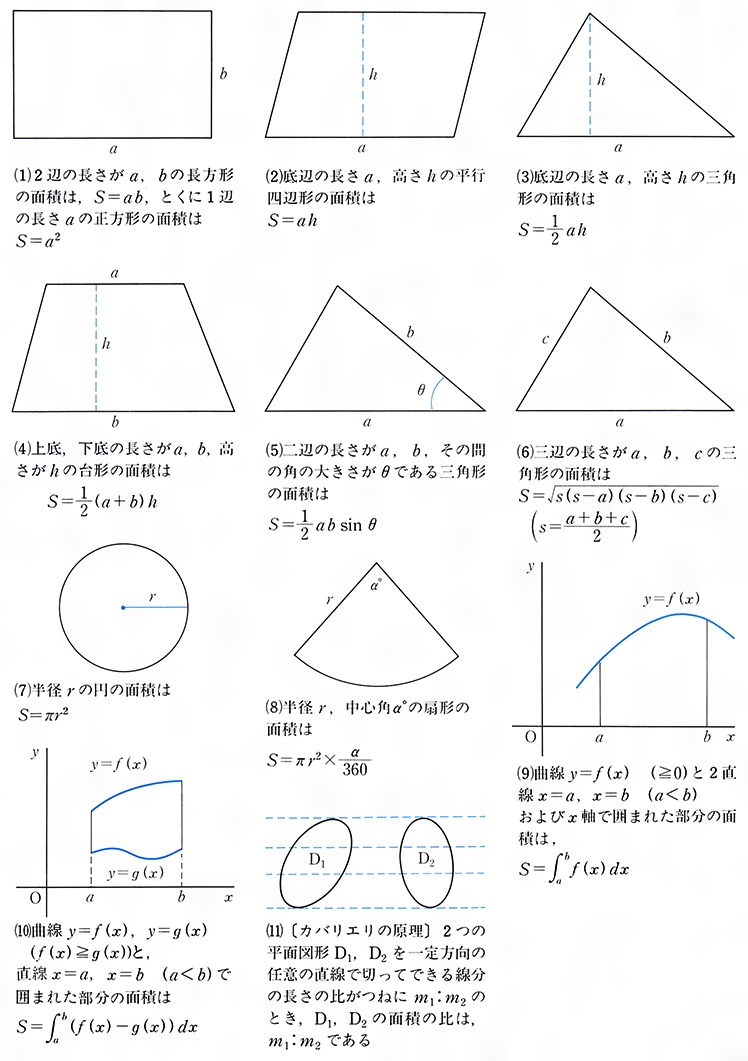



面積とは コトバンク




7月あらたにスタートです 図形の面積をマスターしよう ふるやまんのマスラボ奮闘記
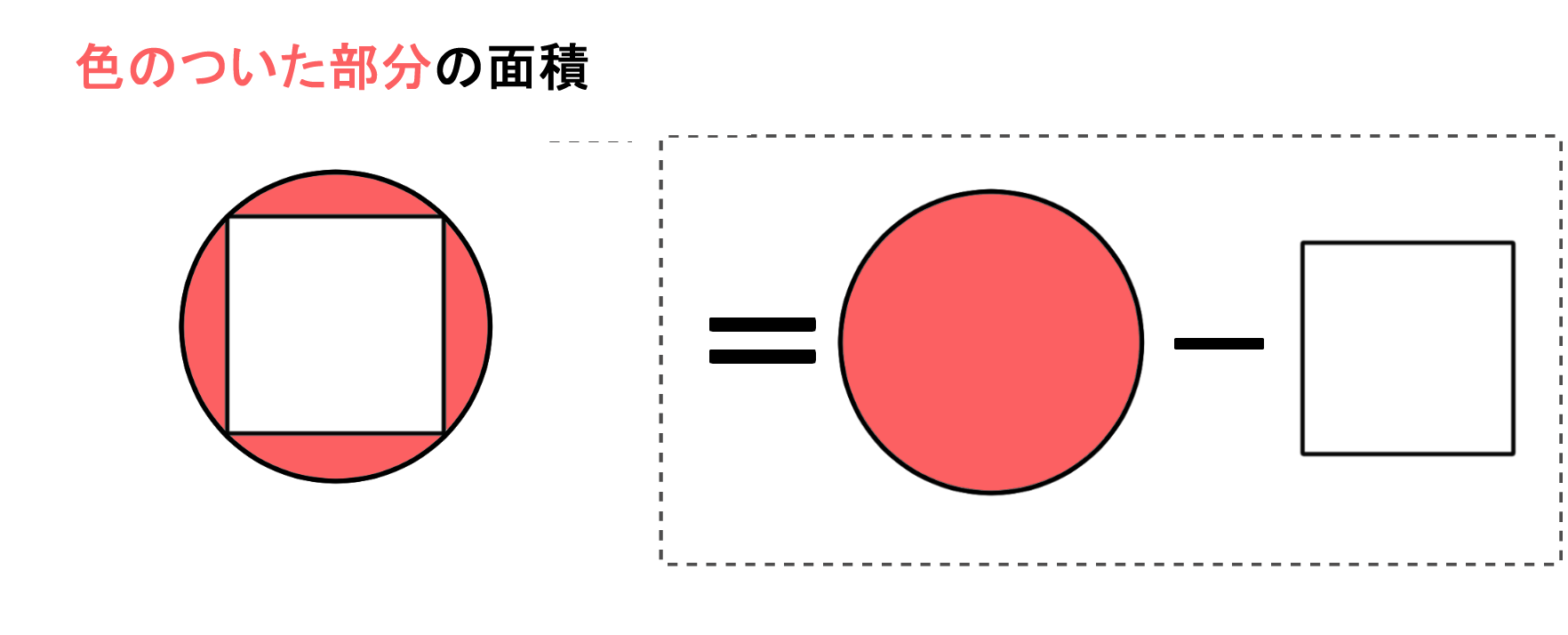



色のついた部分のへんな形の図形の面積を求める問題 バカでもわかる 中学数学



0 件のコメント:
コメントを投稿