√99以上 因数分解 中3 応用 235219

 中3数学 因数分解 第4講 例題2 今回の問題はこちら 次の式を因数分解しなさい。 （1）4x^2^x25 （2）9x^212xy4y^2 解説は下にあります。 "中3 因数分解 第4講 例題3" の 続因数分解の3大パターンをしっかりおさえよう 復習 因数分解の3大パターン （2乗） － （2乗） ＝（x＋a）（x－a） x 2 ＋ （2倍） x＋ （2乗） ＝（x＋a） 2 x 2 ＋ （たし算） x＋ （かけ算） ＝（x＋a）（x＋b） 前回までの内容でも、難関レベルの問題に対応できると思うが、 今回は前回までで触れていない補足問題を扱う。 前回 因数分解の工夫と練習問題(2)(標～難) 次回 展開・因数分解の利用(

高校数学 数 10 因数分解 応用編 Youtube

因数分解 中3 応用

因数分解 中3 応用-多項式と単項式の乗法除法 式の展開 乗法公式 (xa) (xb)の展開 乗法公式 2乗の展開 乗法公式 和と差の積の展開 式の展開 いろいろな計算 式の展開 四則 因数分解1_共通因数をくくりだす 因数分解2_ (xa) (xb) 因数分解3_2乗 因数分解4_ (xa) (xa) 因数分解 おきかえ 共通因数をくくりだした後さらに因数分解 項を分けて因数分解する1 (発展) 項を分けて因数分解する2 (発展)解説 x2 y2 x 2 y 2 は、因数分解できません。 どのように式変形をしたらよいのか。 (xy)2 = x2 2xy y2 ( x y) 2 = x 2 2 x y y 2 を利用します。 これは思いつくものというよりも、知識です。 この式を変形すれば、 (xy)2 = (x2 y2)2xy ( x y) 2 = ( x 2 y 2) 2 x y

中3 二次方程式の解き方 平方根 因数分解 中学数学の方程式 中間 期末テスト 高校入試対策

3年2次方程式(因数分解利用)類題1 2 ⑦ 5 4 16/3/2 3年 2次方程式応用4(4) 解答(誤)100x → (正)100x 16/1/7 3年 三平方の定理2 1(3)〜(5)の図 中1数学の方程式文章題を例題と練習問題で徹底中3の4月に学習する 「式の展開・因数分解」 中2の復習として 「四分位数・箱ひげ図」 の動画講義をお届けします。中3の数学のコツ 数学を山にたとえると、今、君たちは、3年間の数学の学習を通して、中学校の数学の頂上に立っている。 もちろんこれからも、山は続くだろうし、もっと高い山もあるだろう。 しかし、ここで自分の登ってきた道をふり返ってみるのも

 数学宣教師 ザピエル今回は、こんな質問をいただきました！ハムちゃん\( ab(x y) a(y x) \) を因数分解してください数学宣教師 ザピエル最近は、因数分解関係の問題をよく聞かれ2つの応用パターン 0：08 今まで因数分解公式⓪～③を確認しましたが、それに加えて、だいたい 2 つのパターンの問題が載っています。 ①共通因数をくくり出し、かっこの中を因数分解する a x 2 a x − 6 a = a ( x 3) ( x − 2) ②式の一部をまとめて文字に無料 中3数学 発展・応用問題 問題プリント 式の計算5 因数分解1 テキスト マスコン 中3数学 発展問題 (式の計算5 因数分解1) 氏名( ) DQ305 3006次の式を展開して、簡単にしなさい。 3008次の式を因数分解しなさい。

応用因数分解（中学3年） 次の式を因数分解しなさい。 （1）$ (ab1)^2(a1)^2 $ （2）$ x^2y^212x36 $ （3）$ x^2y^2x^2y^21 $ （4）$ xy3x2y6 $ 中学数学 代数分野 式の計算 式の展開と因数分解 連立方程式 文章題 このページでは中3の数学で押さえておきたい 「多項式の計算」「因数分解」「平方根」「二次方程式」 の基礎ポイントをご紹介させていただきます。 こんなページも見られています！ ＞＞中学3年生の教科別学習ポイント 21年4月から中学校の教科書が これが高校数学で覚えておかないといけない因数分解公式です。 中でも、 a2 b2 c2 2ab 2bc 2ca = (a b c)2 a 2 b 2 c 2 2 a b 2 b c 2 c a = ( a b c) 2 a3 b3 c3 − 3abc = (a b c)(a2 b2 c2 − ab− bc −ca) a 3 b 3 c 3 − 3

因数分解 多項式の応用 文章題 中学数学 練習問題プリント 数奇な数

U9j580gf8iba369ji2w Xyz P 599

You're signed out Videos you watch may be added to the TV's watch history and influence TV recommendations To avoid this, cancel and sign in to on your computer Cancel Confirm 因数分解公式3 因数分解 因数分解公式のなかでもわりと理解しやすく、簡単に感じるかもしれません。 この2乗引く2乗の形は今後さまざまな分野で使われるため応用が利くことで特に重要なものです。 2乗の元 (平方根)がすぐに出てくるように 中3の因数分解の応用問題です。 『難問だけどクセになる良問』シリーズ第1弾です。 みなさん解けるかチャレンジしてみてください。では問題です。 問 $ 9991 $ を素因数分解しなさい。 いや〜シンプルな問題ですね〜。

中３生 因数分解の応用 多賀城市 塾 多賀城市の塾 ｙｓｔ進学研究会

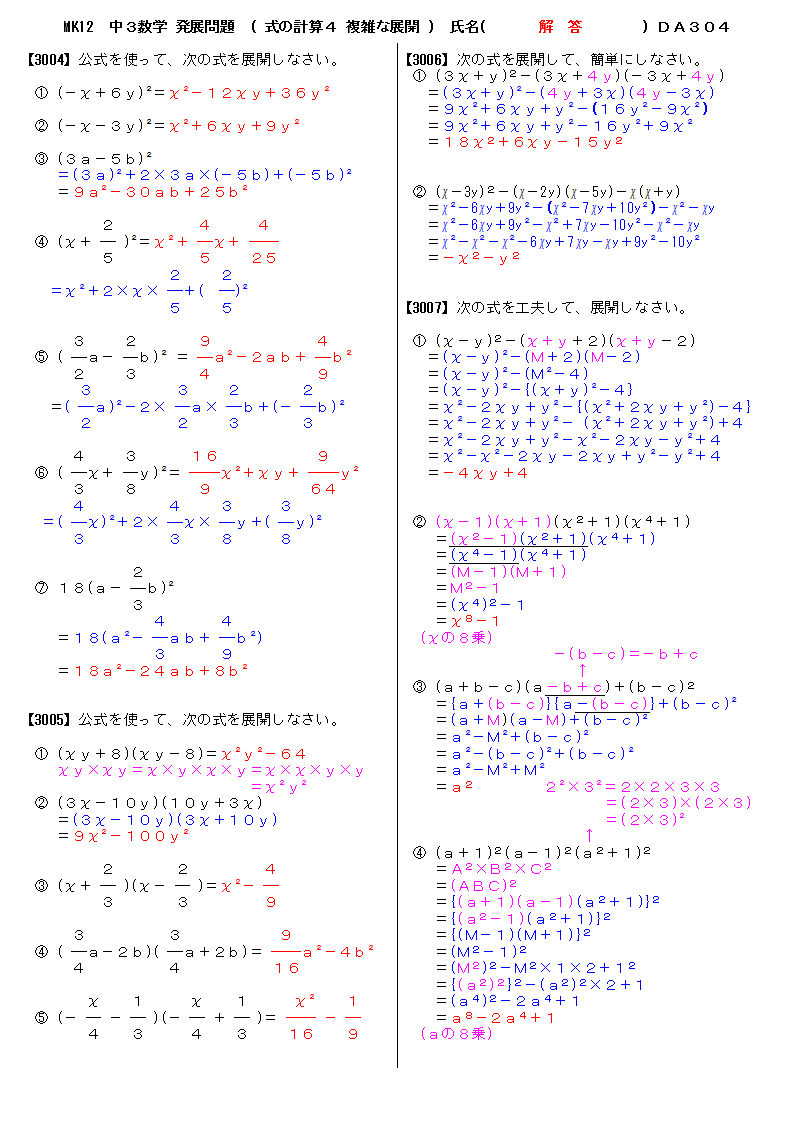
無料 中３数学 発展 応用問題 解答プリント 304 式の計算４ 素因数分解

の形にします． ところで，積が −b 2 bx になるものは何かというと，それは全体の大きな因数分解をしている中で，定数項 −b 2 bx を2つの式の積に分けるということで，それは −b 2 bx をあらかじめ因数分解しておくということです． −b 2 bx=b (x−b) ここで， b (x−b)=x となって和が x になっています． 結局 a 2 x a −b 2 bx = a 2 x a b (x−b) = ( a b) ( a x−b) （答 単元 因数分解, 「因数分解を解く時に 確認しなければならない順番をまとめました。 汚い字ですみません。」, 学年 中学3年生, キーワード 因数分解 中3 因数分解 第8講 例題2 応用レベル 複2次式 今回の問題はこちら 解説は下にあります。 解説はこちら

Mathematics やや難しい因数分解 働きアリ

高校数学復習記録 その2 桜花 現役バイト塾講師 Note

 top3 高校の因数分解を5分でマスター！ 現役塾講師によるラクラク数学講座 8月 25, はぁ、因数分解がなんとなく苦手です。 簡単な問題なら解けるけど、応用問題や3次式の問題になると、とたんに解けなくなる。 もう一度 基礎から学んで 因数分解～基礎から応用まで 高校の数学では，最初に「数と式」という分野を学習します（数学 i ）。 ここでは、単項式や多項式、それに整式、式の展開公式などを学びますが、その次に待ち受けているのが「因数分解」です。 因数分解は、数学 i だけでなく今後の数学でずっと登場す いろいろな因数分解置き換え問題の解き方がわかる3ステップ 因数分解の置き換え問題の解き方を知りたい！？ こんにちは！この記事をかいているKenだよ。爪は大事だね。 因数分解の応用問題の1つに、 置き換え問題 ってやつがいる。

数学 時短演習cote

高校数学 数 10 因数分解 応用編 Youtube

 素数と素因数分解（中3） 素因数分解の応用（約数の個数、平方数）（中3） 公約数と最大公約数（中3） 公倍数と最小公倍数（中3） 単項式と多項式の乗法と除法（中3） 展開と乗法公式（中3） 因数分解とその公式（中3） 平方根とその近似値・大小、有理このページは『多項式・式の計算の利用』‥一般的に言う応用問題の中の証明問題(文章問題)の解説になります。 証明には型のような手順がありますので覚えていってくださいね！ 多項式・因数分解の・共通因数をくくる因数分解中3数学 ・(x＋a)(x＋b)の因数分解中3数学 ・2乗の因数分解中3数学 ・2乗－2乗の因数分解中3数学 05因数分解（2） ・共通因数→公式利用による因数分解中3数学 ・おきかえによる因数分解中3数学 ・複雑な

U9j580gf8iba369ji2w Xyz P 608

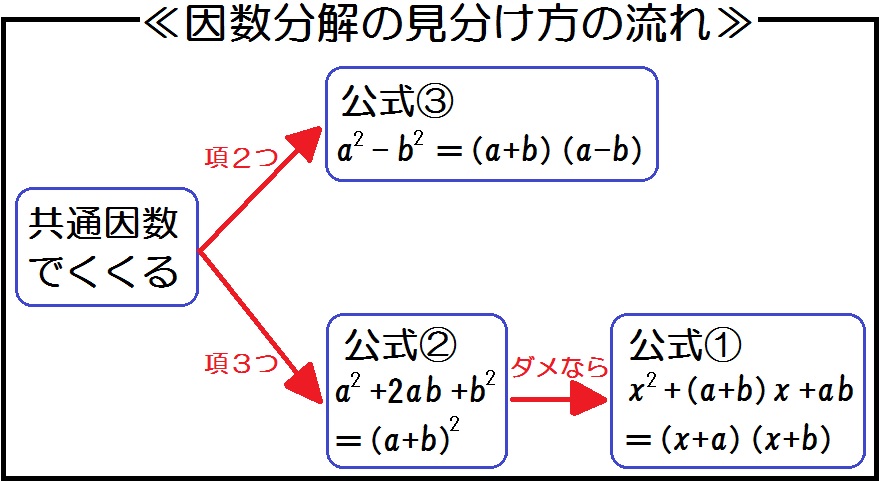
中学数学 多項式 の教え方 因数分解の応用問題

高校の数学Ⅱで扱う因数分解の基本から応用までの練習問題です。 因数分解は展開の逆演算です。 展開は乗法公式を覚えていなくても必ずできますが、因数分解は基本公式を覚えていないとできません。 応用となると少し手を加えないと先 因数分解は途中で終わってはダメです｡ とにかくいけるところまできれいに因数分解しないと、容赦なく×になってしまうので注意しましょう｡ 何かの2乗があるときは､まだ因数分解できるのではないかと疑う癖を付けるといいですね｡ ②\( (x^23)^24x^2\) 中3数学では、 因数分解 をならうよ。 じつはこれ、けっこう重要な単元なんだ。 因数分解の問題がよくでることはもちろん、 二次方程式をとくためにも必要だからね。 もう、ぶっちゃけ、 因数分解を制するものは中3数学を制する といっても過言じゃ

中３ 式の計算 因数分解 応用編 基本の理解で組立ｏｋ 難問と勉強の取組みについて 教えたい 人のための 数学講座

中学数学の解説5ページ目 三重の個人契約家庭教師

 中学3年生 中学校3年生の展開･因数分解を利用した応用問題を解いたノートです。 授業ノートなので見にくいところはあしからず spというのは先生が作ってくださったオリジナルのスペシャル問題という意味です。 中3数学「多項式」の5回目。今回は因数分解の応用問題のやり方を解説します。応用問題とは、こんなの↓ 例21）\( 3x^2 75 \) 例31）\( (x1)^2 4(x1) 3 \) 例41）\( 2a(b5) 今回は標準レベル上位から難関レベルの因数分解を見ていこう。 高校入試の因数分解では難問に含まれる問題も少し扱う。 前回 因数分解の工夫と練習問題(1)(標~難) 次回 因数分解の工夫と練習問題(3)(難)

中３ 展開と因数分解２ 多項式と単項式の除法 予習 中学数学の勉強に

中3 二次方程式の解き方 平方根 因数分解 中学数学の方程式 中間 期末テスト 高校入試対策

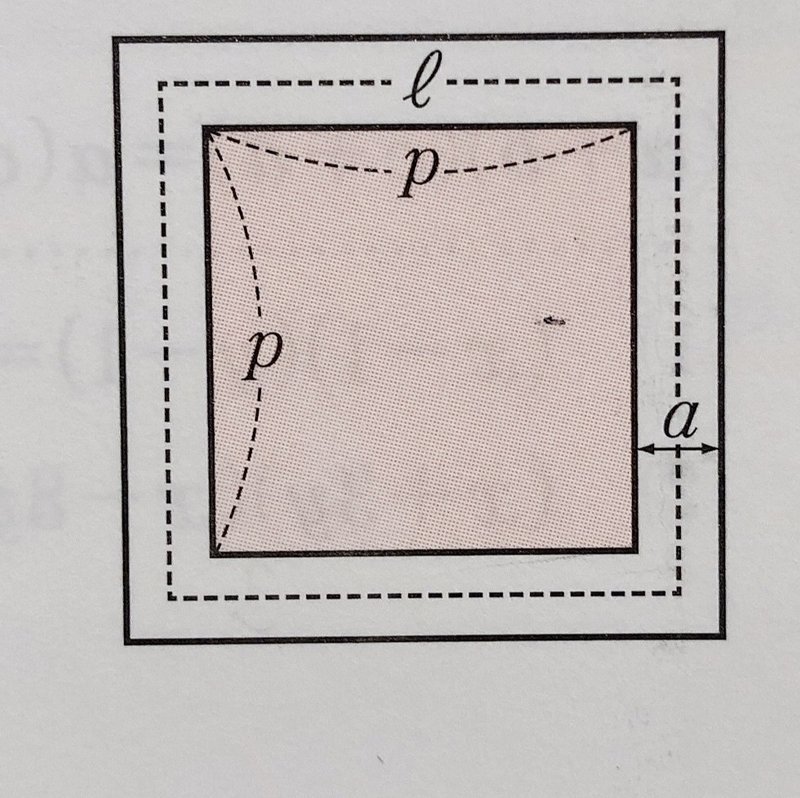
中3数学因数分解の応用問題質問の解説 ⚡ これから学ぶのは、その展開されているものを、かけ算のかたちに直す因数分解です。 長々と説明しましたが、結局は2つある を消すことが出来る数字を入れてあげれば、解が得られるということです！ 道の面積を表すためにはa×ℓですが、ℓを別の表し方をします。 ℓとは道の真ん中の線ですよね、それをaとPを使って表す。 角っこの部分を見ると下の図のように赤で表したところは実はaになります。 角は4つあるので4×aで4a 残りの点線の部分はP×4つなので4P 2つを足すと「4a＋4P」になりこれがℓの別の表し方になります。 つまり S＝aℓ＝ a（4a＋4P） ．．．①X 2 − y 2 − 12 x 36 = x 2 − 12 x 36 − y 2 と、項の順番を入れ替えたらどうだろうか。 前3つの項が因数分解できる。 x 2 − 12 x 36 − y 2 = ( x − 6) 2 − y 2 すると、なんと中抜けの形式が浮かび上がった！ x − 6 = A と置くと、 ( x − 6) 2 − y 2 = A 2 − y 2 = ( A y) ( A − y) よって、 ( A y) ( A − y) = ( x − 6 y) ( x − 6 − y) ・・・（答） （3） x 2 y 2 − x 2 − y 2 1

中３数学 式の展開 因数分解がスラスラ解ける 魔法の授業 学校 塾 家庭教師の１カ月分が１本の動画に On Vimeo

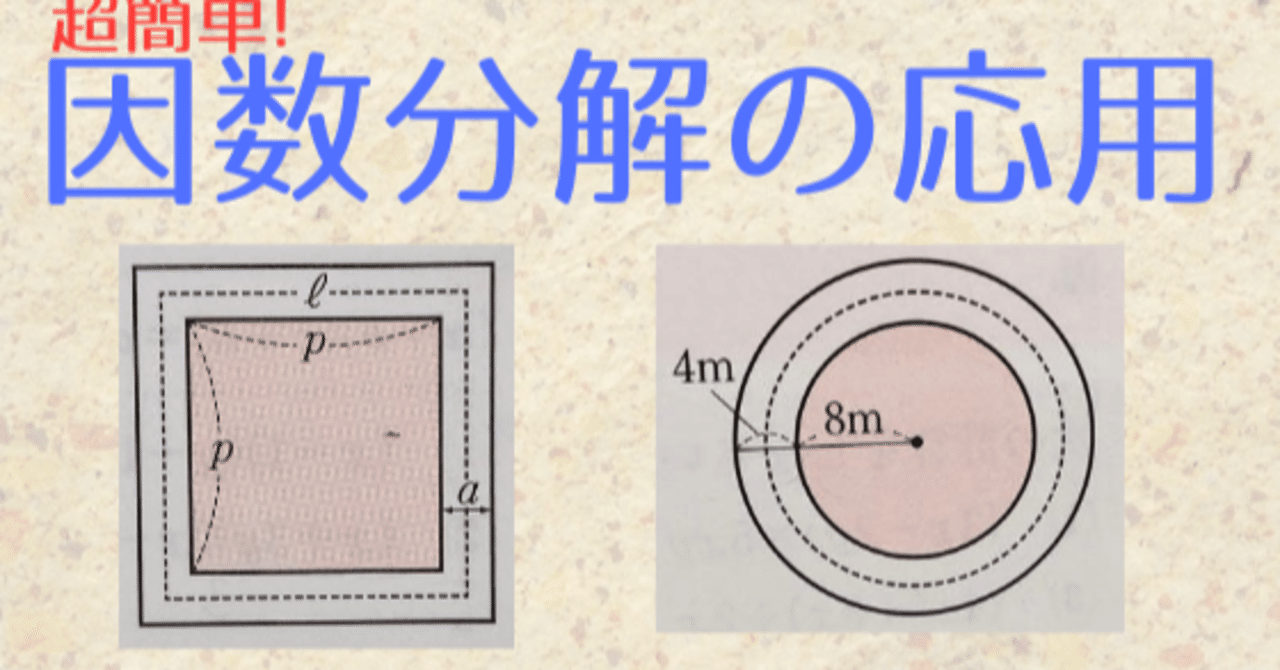
中3数学 因数分解の応用 算数オンライン家庭教師 倉永 将太朗 Note

中３数学１ １５ 因数分解の応用問題にチャレンジ Youtube

数学 中3 6 因数分解 Youtube

数学 質問解答 因数分解の難問 共通因数をくくる問題 中学数学 中３ 因数分解 質問ありがとうございました 行間 ぎょうのあいだ 先生

Studydoctor２乗の因数分解 中３数学 Studydoctor

中3数学 因数分解の応用 算数オンライン家庭教師 倉永 将太朗 Note

U9j580gf8iba369ji2w Xyz P 614

Studydoctor共通因数 公式利用による因数分解 中３数学 Studydoctor

中学3年数学 因数分解 因数分解をわかりやすく解説 高校入試出題率１００ 数学の面白いこと 役に立つことをまとめたサイト

因数分解 多項式の応用 文章題 中学数学 練習問題プリント 数奇な数

U9j580gf8iba369ji2w Xyz P 580

高校数学1の因数分解の応用編の問題なのですが 下の写真の 2 と 3 の Yahoo 知恵袋

無料 中３数学 発展 応用問題 問題プリント 309 式の計算９ 計算の利用２

展開 因数分解の利用 図形 清水塾

中学3年の数学 動画 因数分解 もっと応用編の問題 19ch

中学数学 中3因数分解 数樂管理人のブログ

中３数学の素因数分解の問題 N2乗 24 N2乗 18がともに自然数になるnとは メモ帳

中３ 展開 因数分解の応用 トリセツ終わった人へ Nikkeyweb Rede Da Comunidade E Da Cultura Japonesa No Brasil

1

Amazon Co Jp プロ家庭教師が教える中学生用学習dvd 数学 中学3年 応用 1 因数分解 Dvd 授業 テキスト 問題集 Pcソフト

中3数学 道路の面積を求める問題 例題編 映像授業のtry It トライイット

中3 中3数学 式の計算 素因数分解と因数分解 中学生 数学のノート Clear

因数分解のいろいろな計算 無料で使える中学学習プリント

中学３年 数学 清水塾

中学３年数学 複雑な式の因数分解 Youtube

中学3年の数学 動画 因数分解 ちょい応用編の問題 19ch

因数分解の工夫 中2 中3 中学生 数学のノート Clear

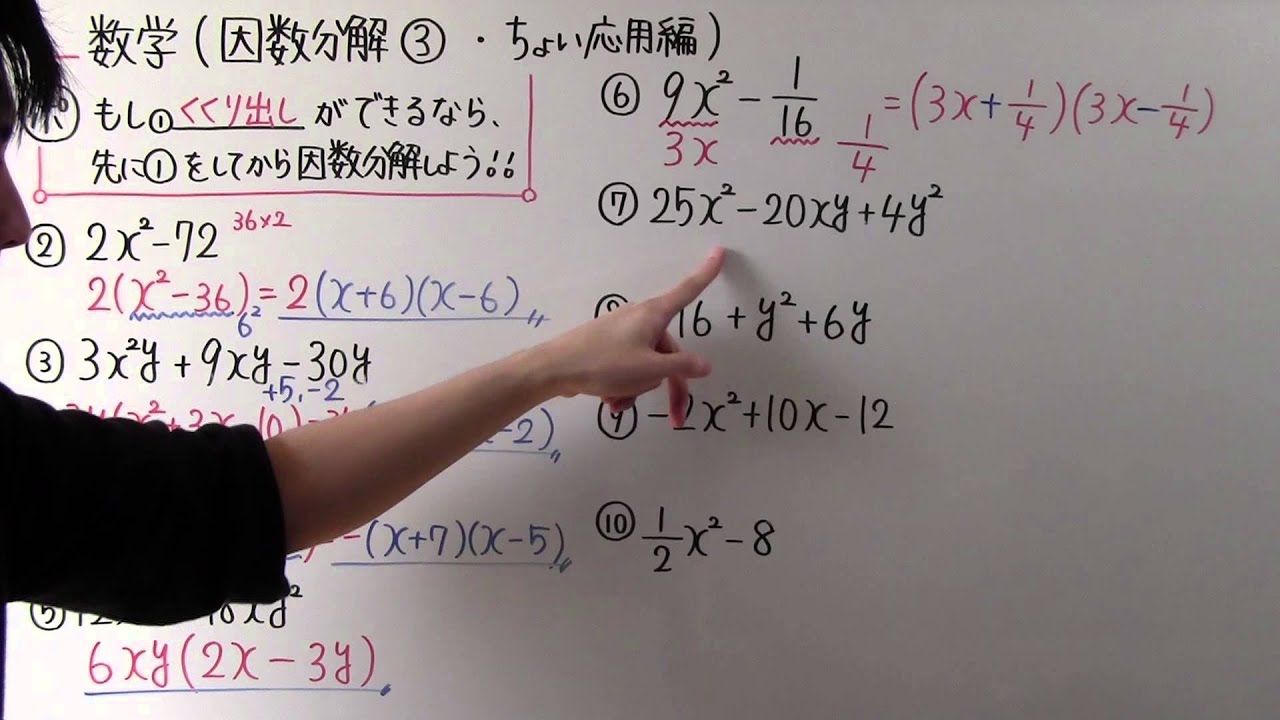
数学 中3 8 因数分解 ちょい応用編 Youtube

中学数学3年 素数と素因数分解 受験の月

中3 中3数学 式の計算 素因数分解と因数分解 中学生 数学のノート Clear

中3数学 02 11 因数分解応用 共通因数と公式 Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト

数学 中3 9 因数分解 もっと応用編 Youtube

Q Tbn And9gcts6i9szgdmycnu8ime9mr7g 4 Whhun5zhnp0 Wz7sfoeincw Usqp Cau

素因数分解のやり方のコツとは 応用問題３選も簡単に解けます 遊ぶ数学

素因数分解 無料で使える中学学習プリント

Studydoctor共通因数をくくる因数分解 中３数学 Studydoctor

中学３年数学練習問題 式の利用 証明 式の展開 因数分解の応用

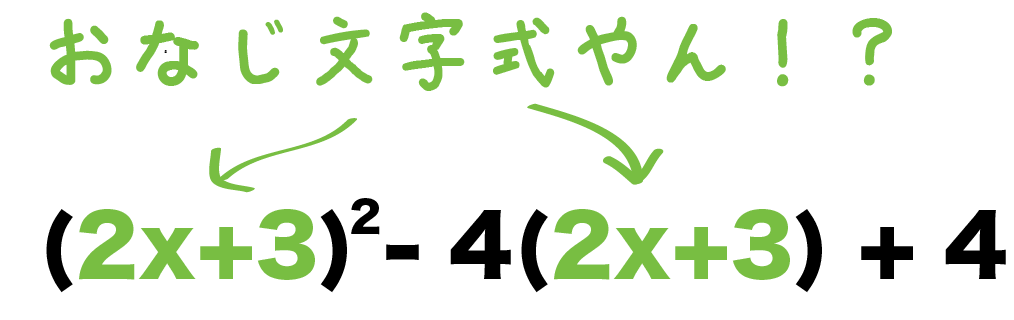
いろいろな因数分解 置き換え問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

中３ 展開と因数分解８ 動画 いろいろな展開 レベル３の解説 中学数学の勉強に

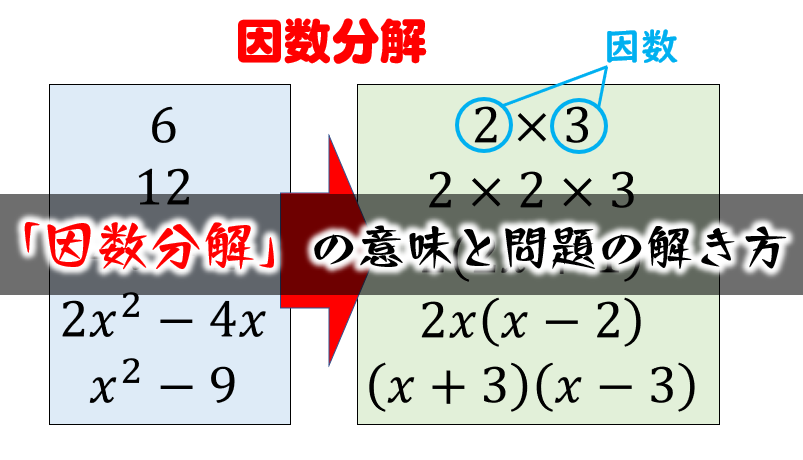
因数分解の意味 問題の解き方 数学fun

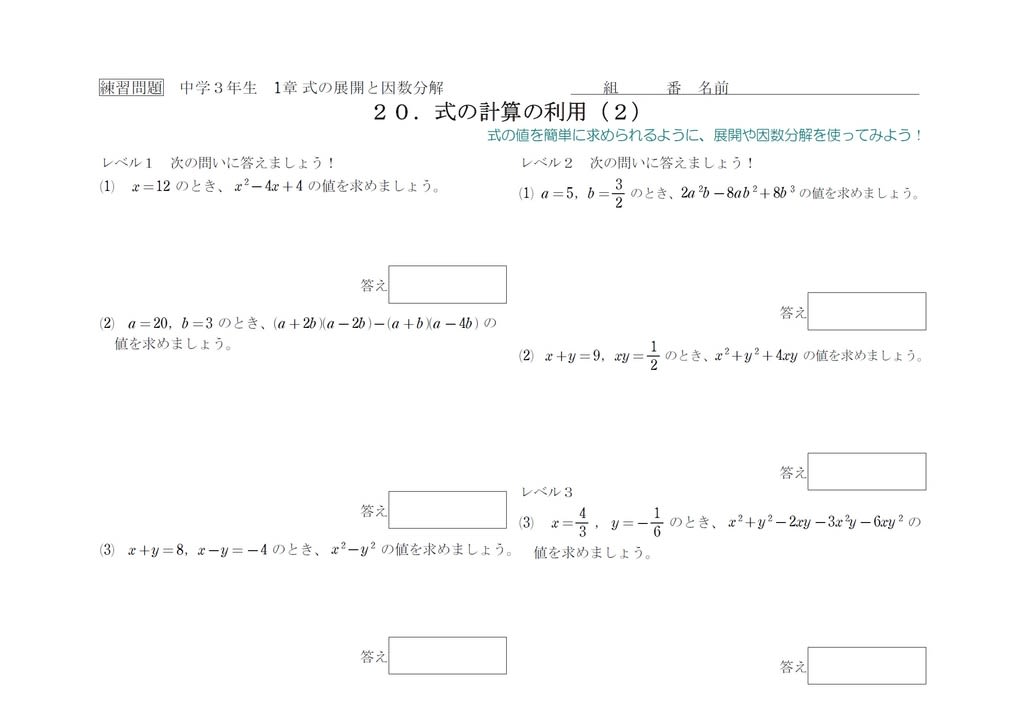
中３ 展開と因数分解 動画 式の計算の利用２ 解説 中学数学の勉強に

中３ 式の計算 因数分解 公式編 設計図の選び方と使い方 あとはパズル 教えたい 人のための 数学講座

中3数学 因数分解の定期テスト対策応用問題 Pikuu

高校入試 難関校の因数分解を解説 Youtube

中3因数分解の応用問題です 25 2 24 2 23 2 22 2 Yahoo 知恵袋

3

因式分解公式

中3数学 因数分解 応用問題 2つのパターンを身につけよう たけのこ塾 勉強が苦手な中学生のやる気をのばす

中学３年生 数学 因数分解 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

中学３年生 数学 因数分解 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

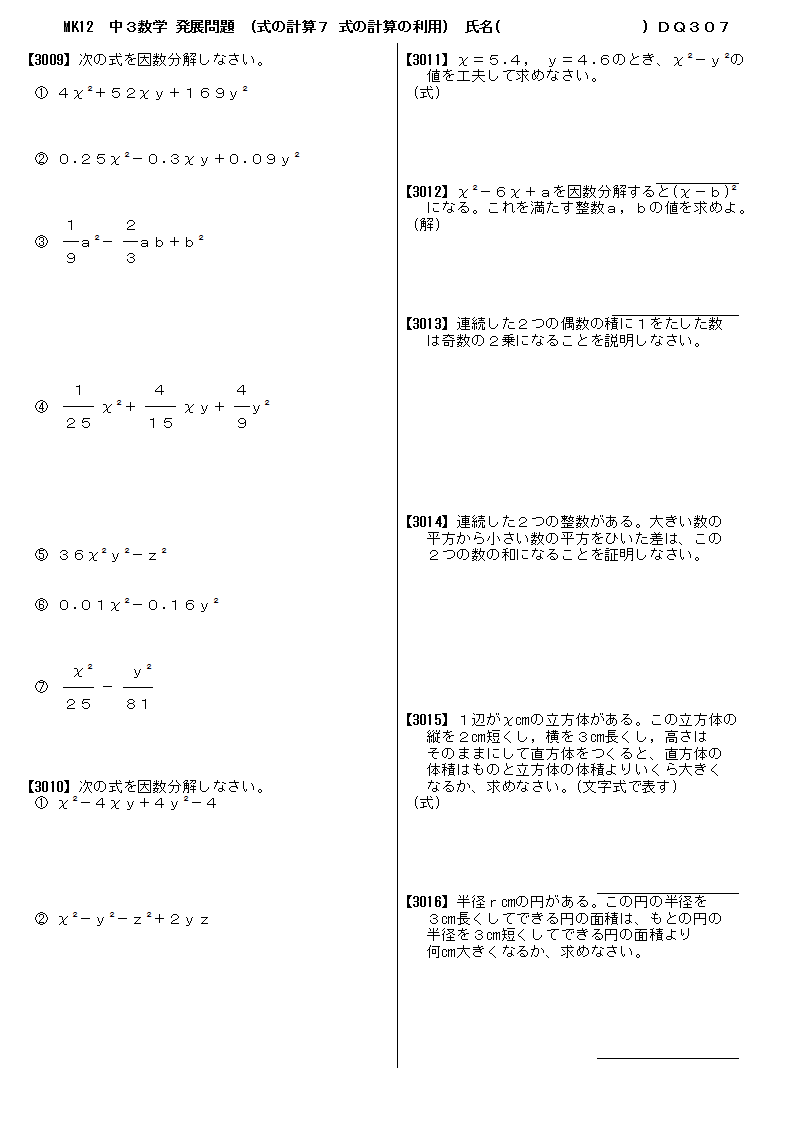
無料 中３数学 発展 応用問題 問題プリント 307 式の計算７ 式の計算の利用

3

中学３年数学練習問題 式の利用 証明 式の展開 因数分解の応用

数と式の問題 京極一樹の数学塾

素因数分解を利用する応用問題の解き方 現役塾講師のわかりやすい中学数学の解き方

Studydoctor複雑な式の因数分解 中３数学 Studydoctor

中3 因数分解 応用 難問だけどクセになる良問シリーズ 第1弾 マスムネのブログ

因数分解の解き方や問題 中学３年生の方は 必見 三重の個人契約家庭教師

中学生のテスト対策プリント 数学編 中3 式の展開と因数分解 学びの森

中３ 数学 因数分解の応用 東京都稲城市の個別塾 学習塾 ナビ個別指導学院 稲城校ブログ

中3の素因数分解を利用した応用問題なのですが Clear

数学 因数分解 いんすうぶんかい とは なぜ因数分解するの そのメリットについて知りたいあなたはこちらをどうぞ 中学数学 中３ 因数分解 行間 ぎょうのあいだ 先生

因数分解とは 公式や計算のやり方 問題の解き方 受験辞典

いろいろな因数分解 2つの応用パターン 教遊者

中学校3年生式の展開 因数分解分野応用問題 中学3年生の数学の授業で Yahoo 知恵袋

中3 中3数学 式の計算 素因数分解と因数分解 中学生 数学のノート Clear

因数分解の応用問題の解き方 現役塾講師のわかりやすい中学数学の解き方

中学数学 多項式 の教え方 因数分解の応用問題

中３ 式の計算 因数分解 応用編 基本の理解で組立ｏｋ 難問と勉強の取組みについて 教えたい 人のための 数学講座

因数分解の工夫 2 標 難 組み合わせ 難 二乗 二乗 最低次数整理 数学の解説と練習問題

至急 中3 因数分解 応用 96 3 96 28 93 2 93 3 3 の式を工夫し 中学校 教えて Goo

中学数学3年 素因数分解の応用 約数の個数 平方数 受験の月

國三 Junior High数学的 中3数学 いろいろな因数分解 筆記 Clear

素因数分解 無料で使える中学学習プリント

中学３年 ７月 ２週 因数分解の応用 ハゲちゃんの算得計算 数得計算

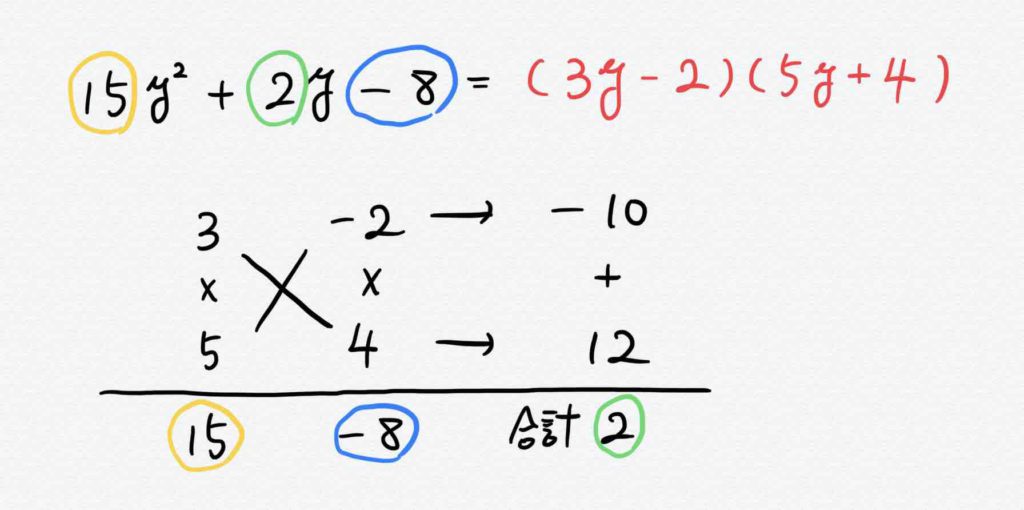
公式いろいろ 因数分解のいろいろな問題とその解き方 スタディクラブ情報局

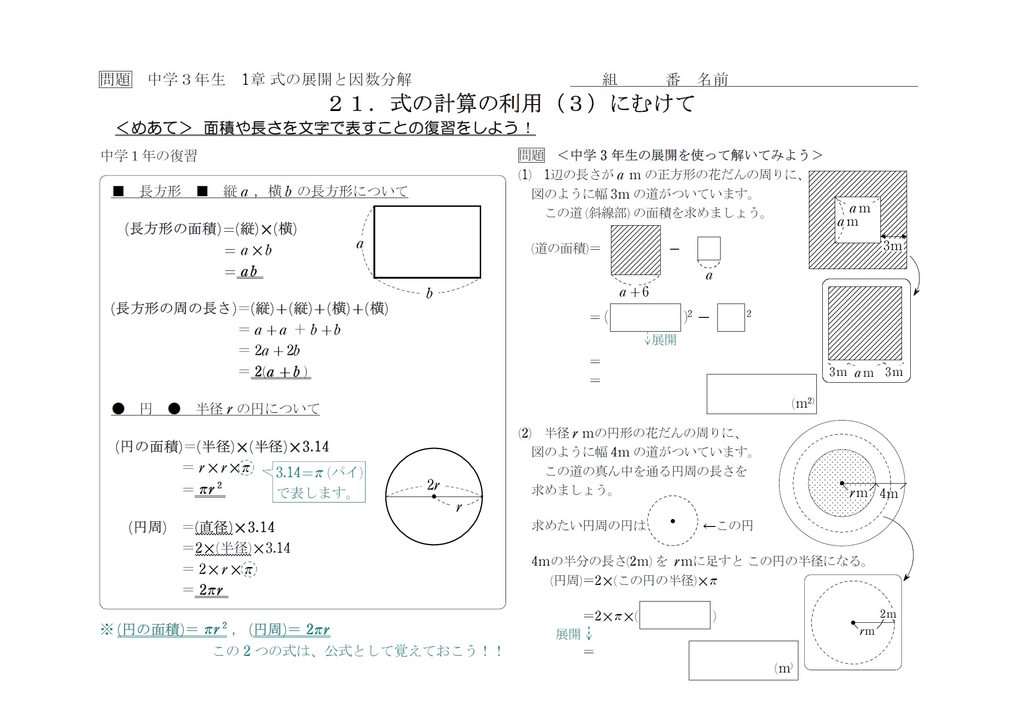
中３自習 展開と因数分解 １ 中学数学の勉強に

いろいろな因数分解 2つの応用パターン 教遊者

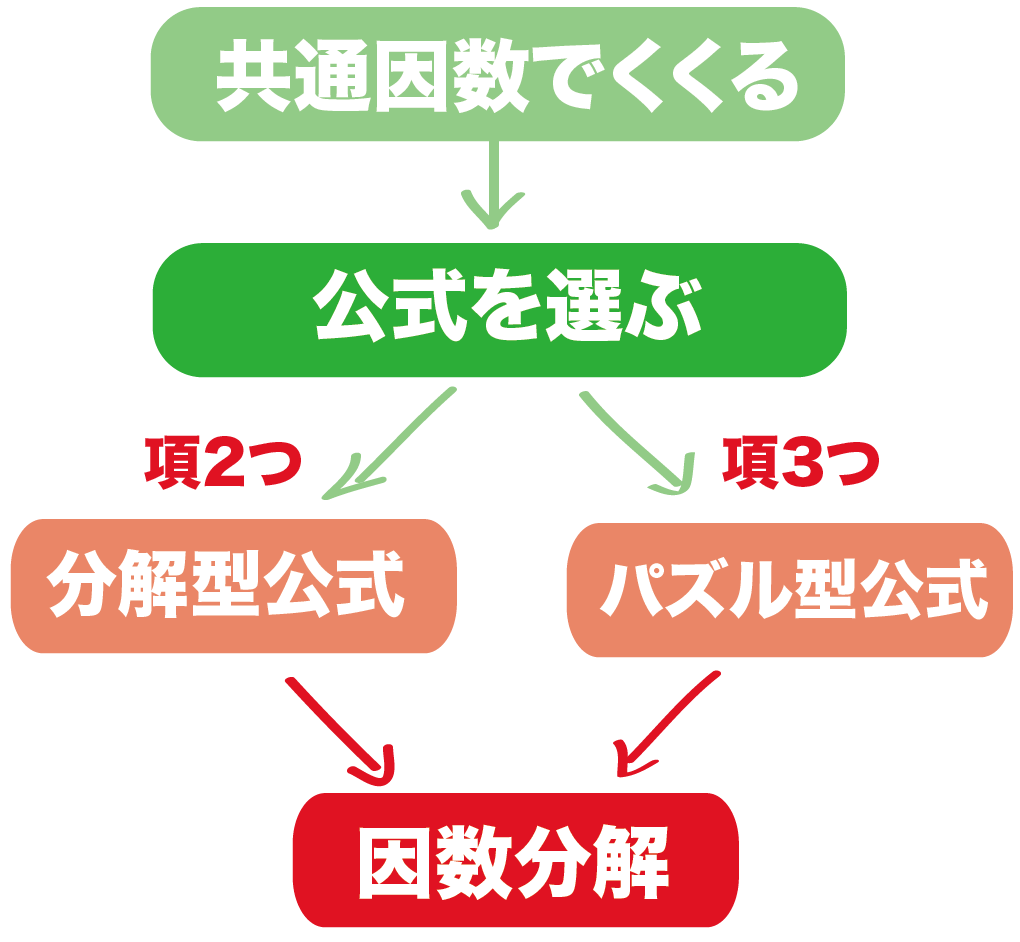
中学数学 因数分解の簡単な解き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

無料 中３数学 発展 応用問題 問題プリント 305 式の計算５ 因数分解１

因数分解の公式のまとめ 中学生はこのパターンを覚えておこう 中学や高校の数学の計算問題

中３ 数学 因数分解７ 因数分解の応用１ ５分 Youtube

中3数学 因数分解はどう解くの 展開 因数分解の 解き方 教え方 いっしょに勉強しよ

素因数分解の応用問題の解き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

展開因数分解の式の値の応用 対称式と交代式 中3数学 高校受験ラボ

素因数分解のやり方のコツとは 応用問題３選も簡単に解けます 遊ぶ数学

中学数学 多項式 の教え方 因数分解の応用問題

これで大丈夫 素因数分解のやり方と応用

高校数学 因数分解の工夫 置き換え 受験の月