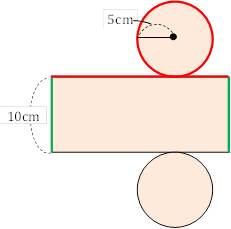
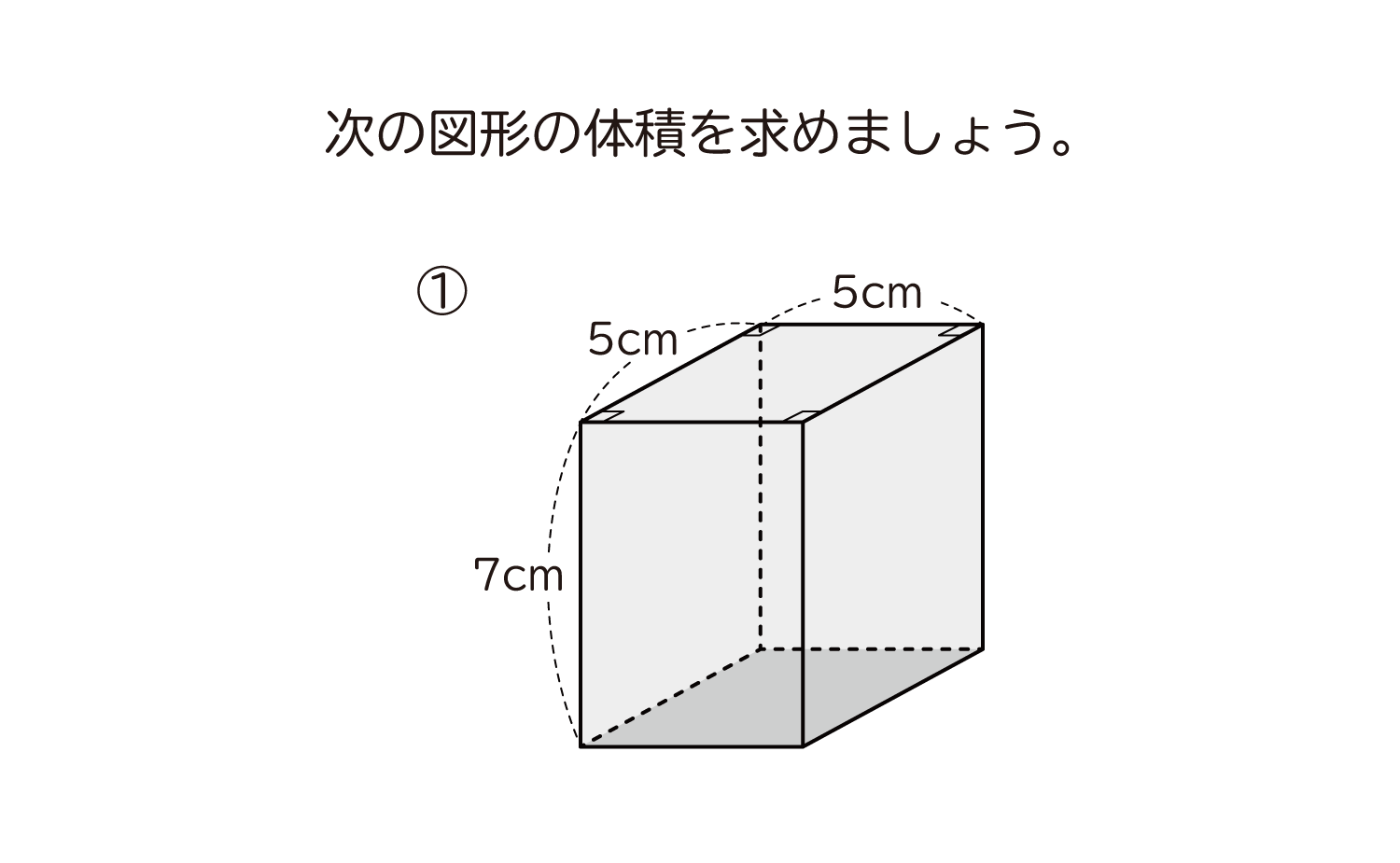
22年(令和4年)度東京都公立高校入試問題前期の数学第5問の問題と解説です。 第5問は空間図形の問題です。 動点があるので関数がらみに見えますが、条件によって固定されています。 ただ、体積の求め方は見方によって難
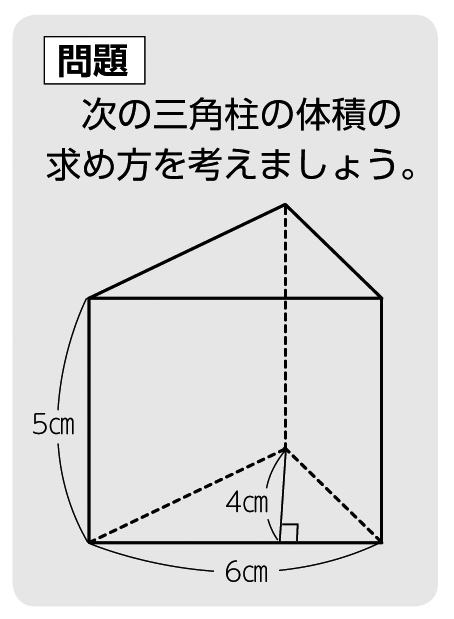
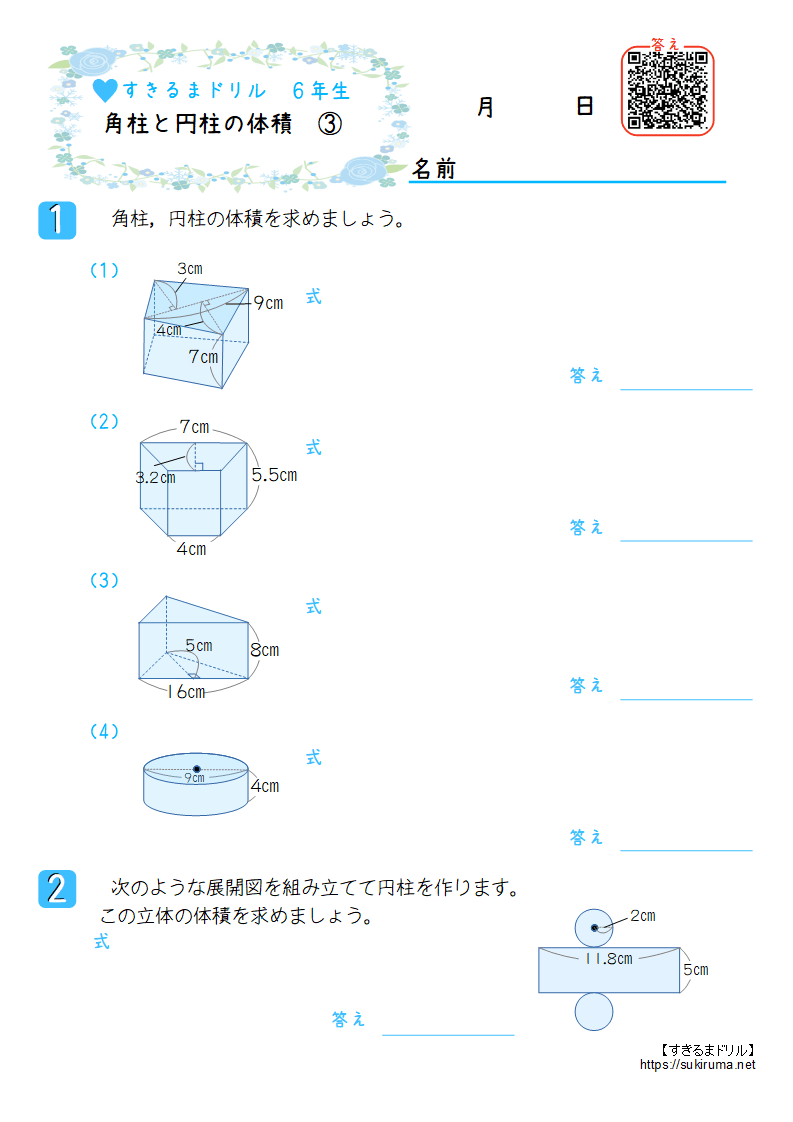
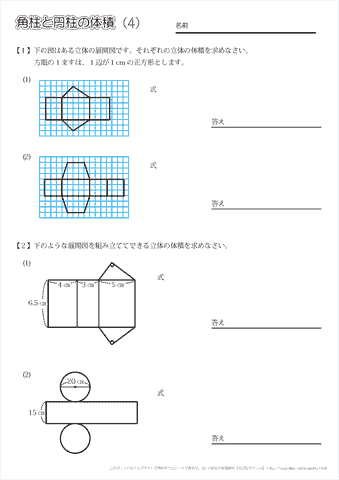
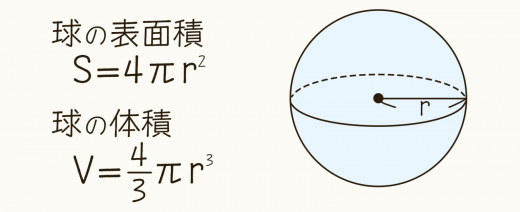
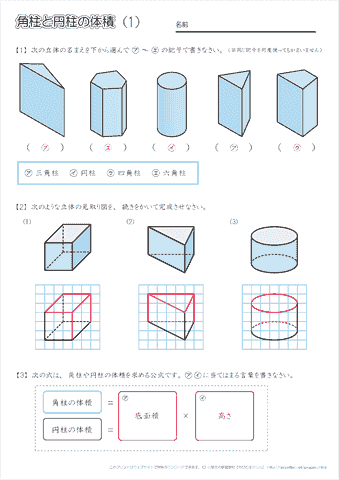
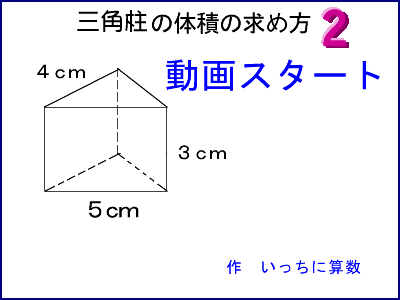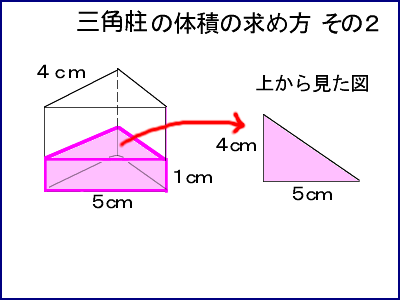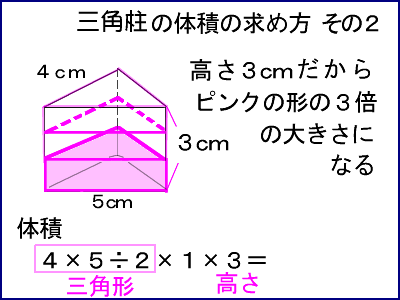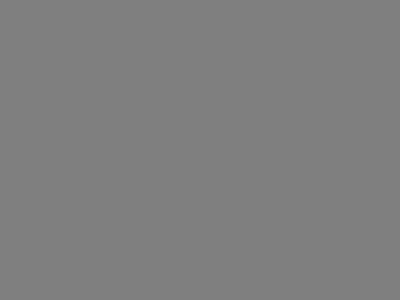
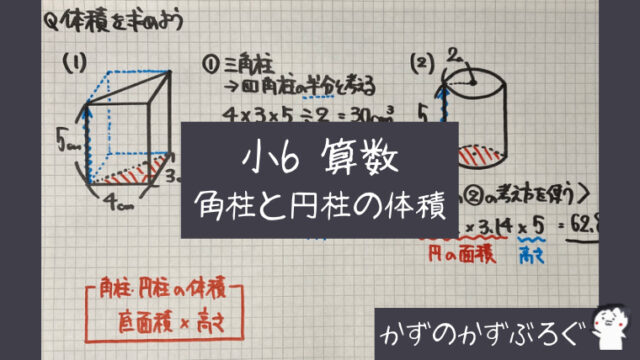
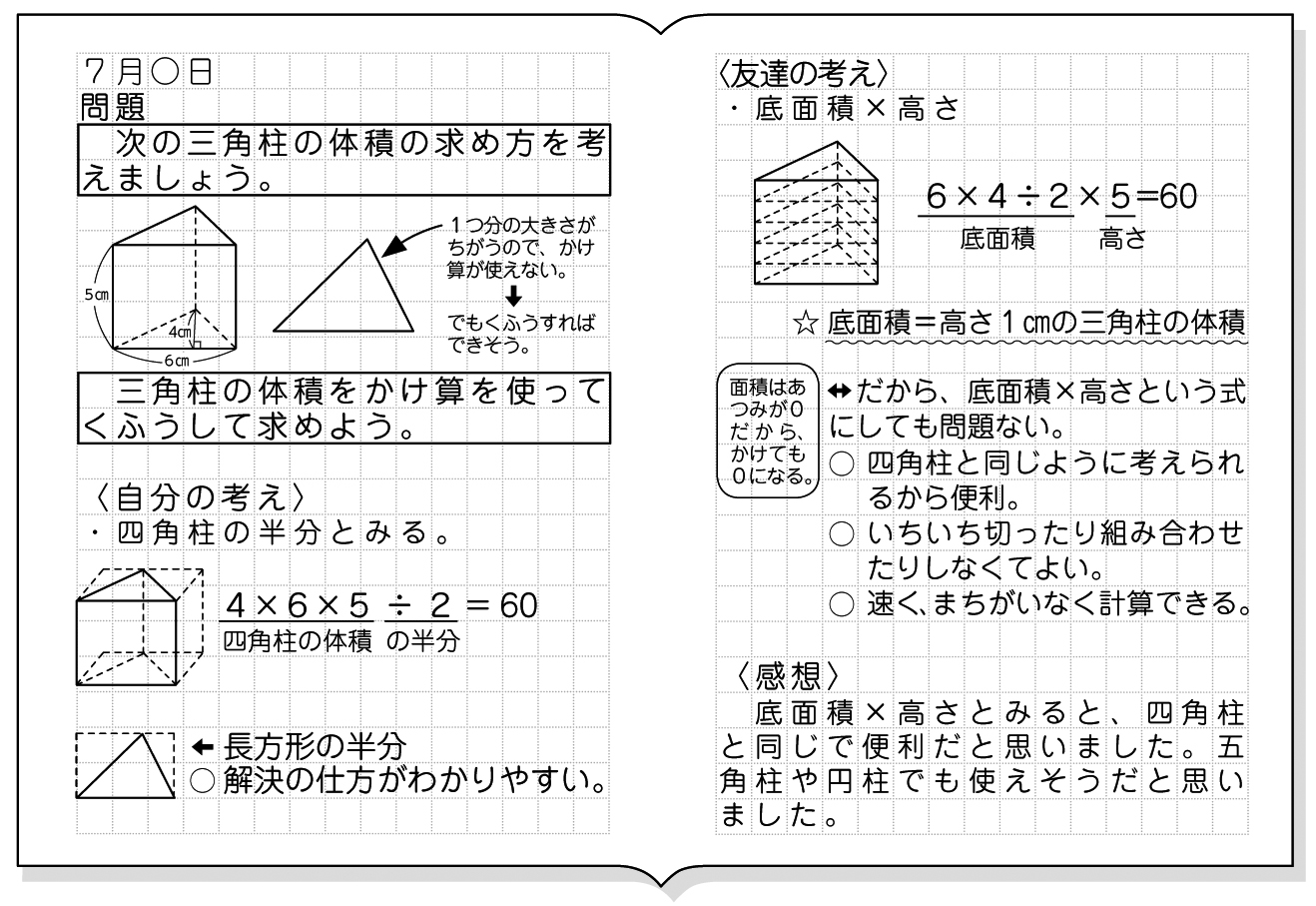
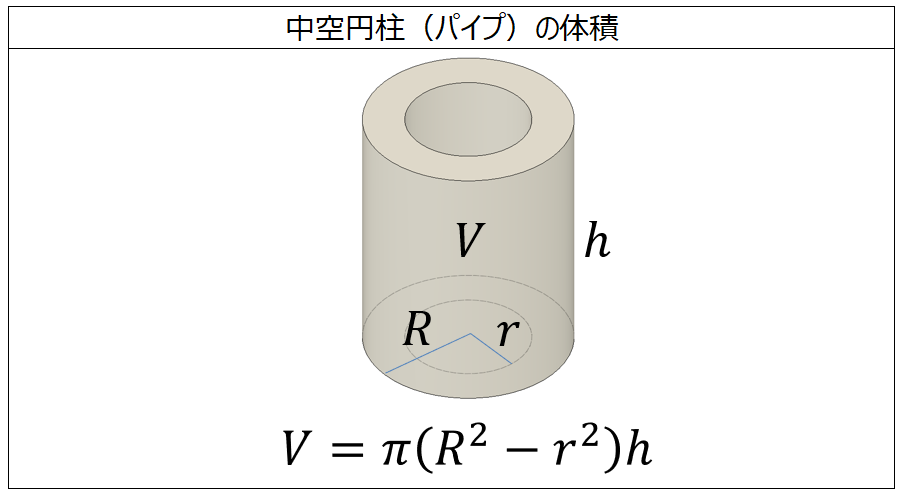
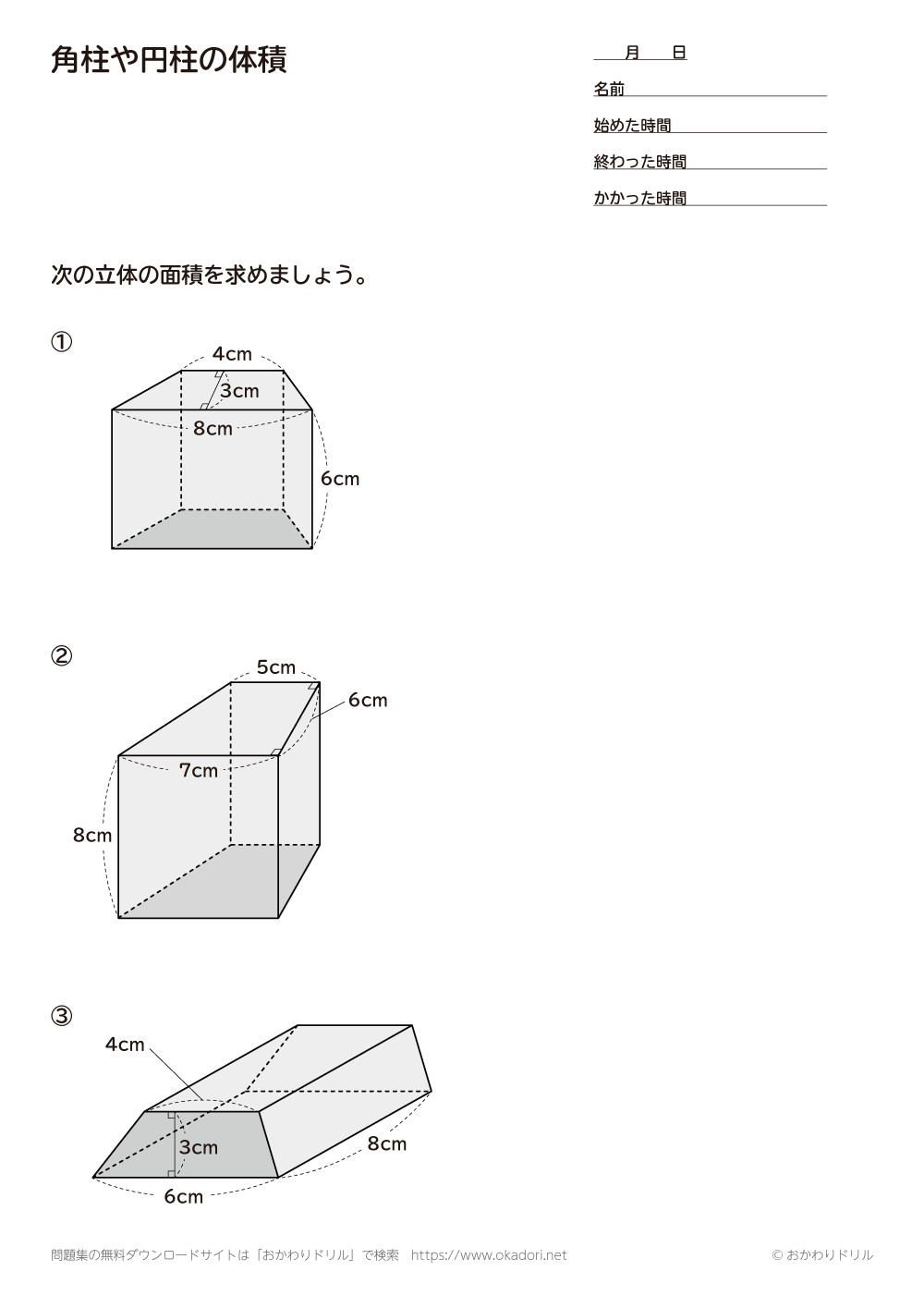
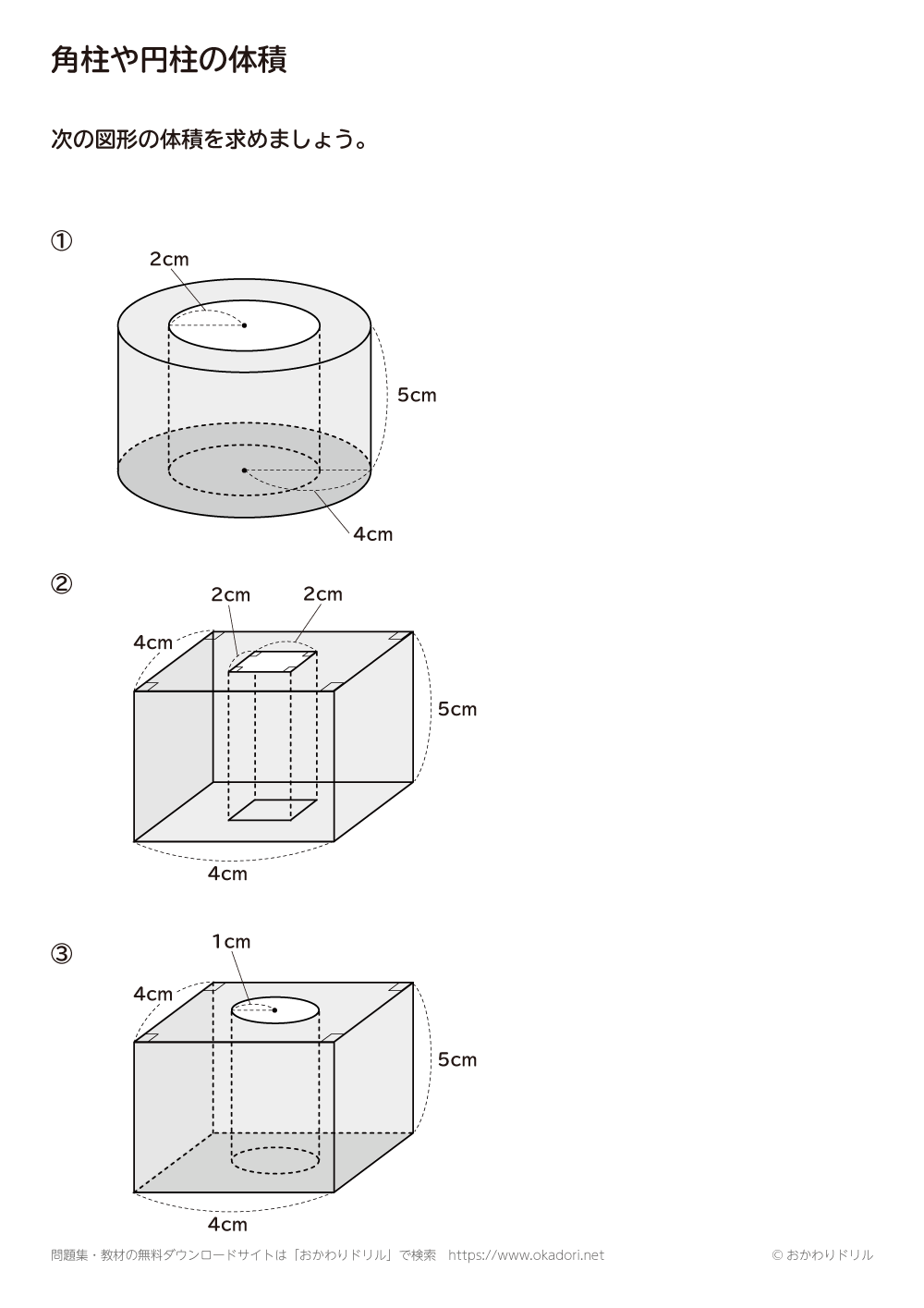
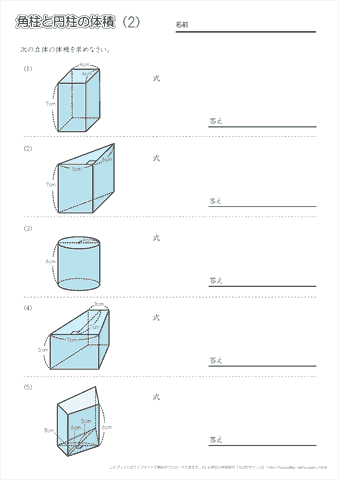
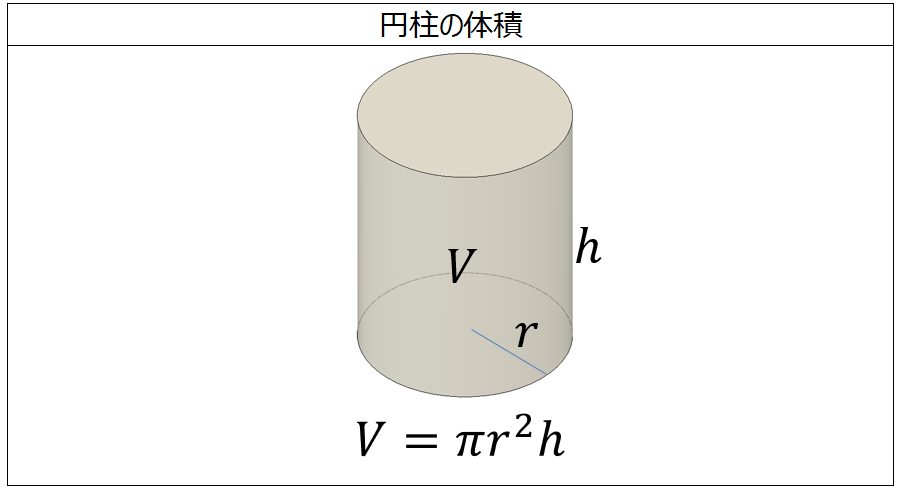
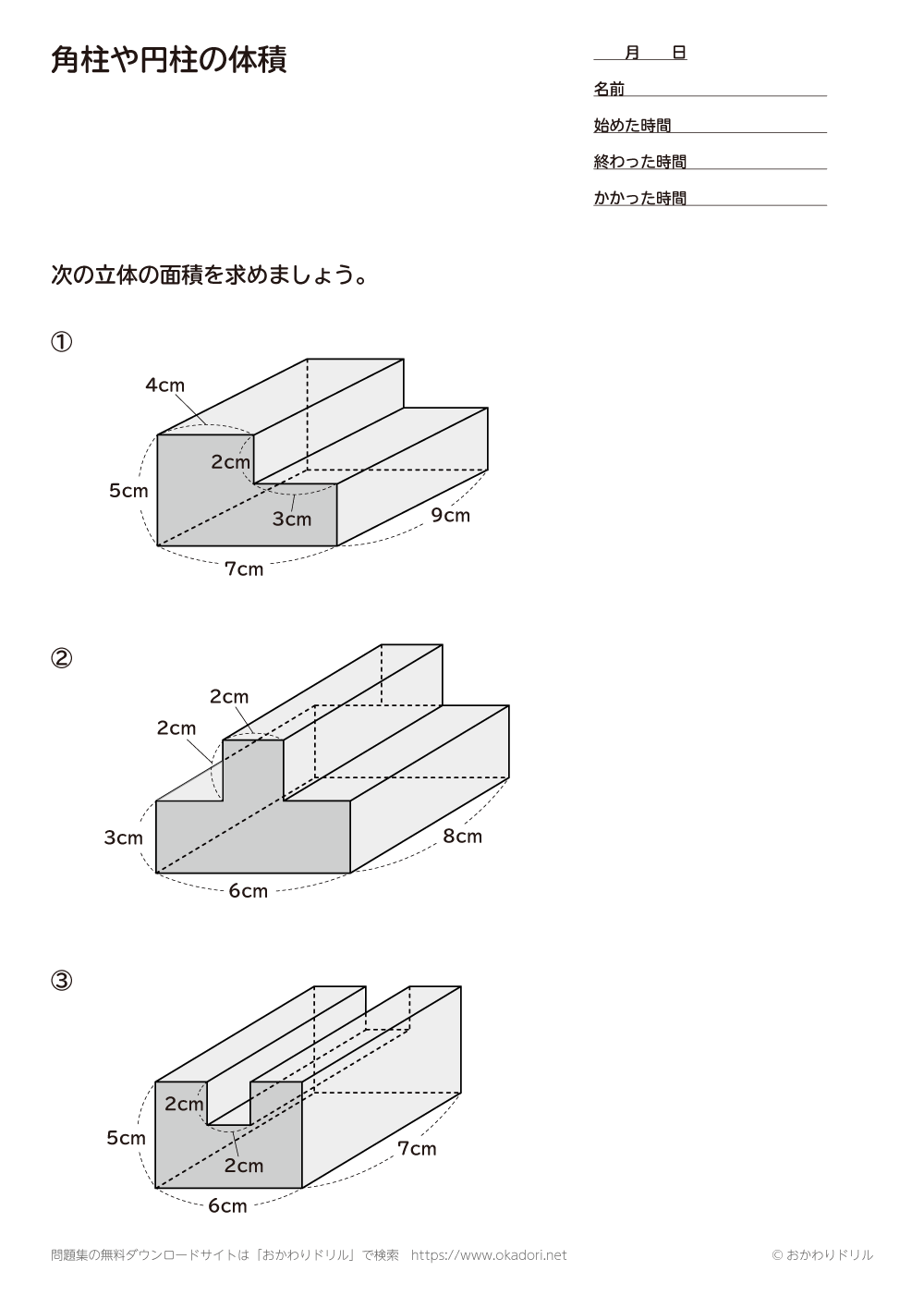
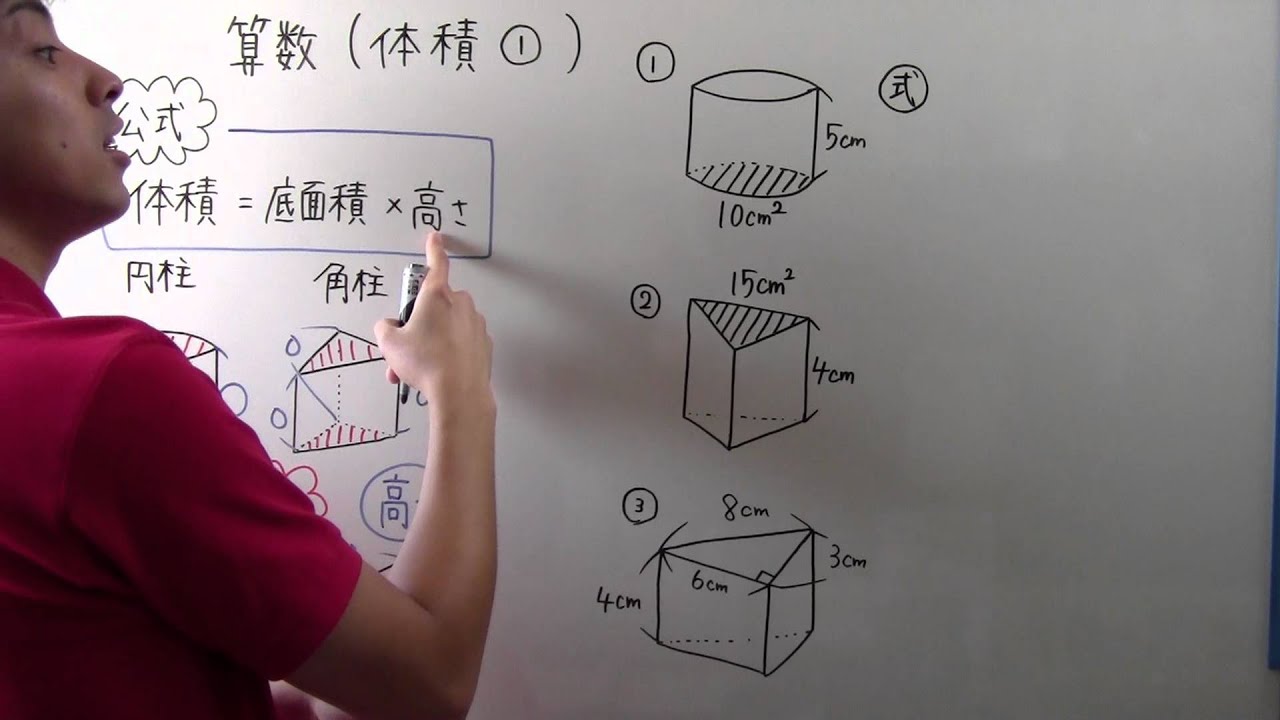
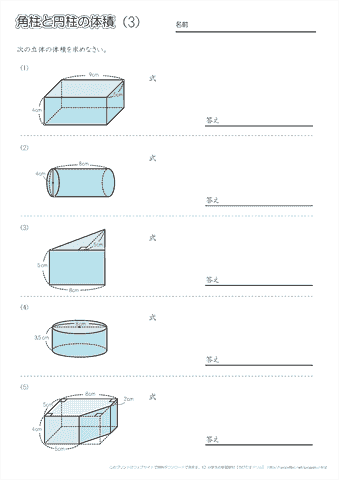
体積の求め方 円-よって、底面の半径 $r$、高さ $h$ の円柱の体積 $V$ は、次の式で求められます。 円柱 (えんちゅう) の体積 \begin{align*} V = \pi r^2 h \end{align*} 体積 = 半径 × 半径 × 314 × 高さ 公式の 導出 (どうしゅつ) 方法と計算例は、「円柱の体積の求め方」をご覧ください。 角柱の体積の求め方は、公式に当てはめるのが一番簡単です! 角柱の体積 = 底面積×高さ 角 柱 の 体 積 = 底 面 積 × 高 さ この公式で求めることができます。 では問題を1問解いてみましょう。 図の三角柱は底面が三角形のため、底面積を以下の式で
体積の求め方 円のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  |  |
 |  | |
「体積の求め方 円」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「体積の求め方 円」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
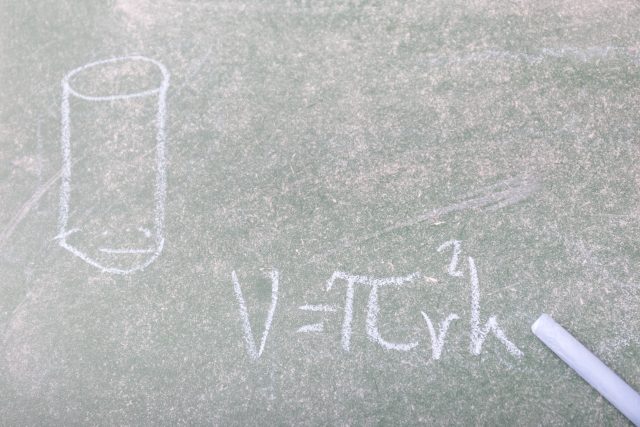 |  | |
 |  |  |
 |  | |
「体積の求め方 円」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  | |
「体積の求め方 円」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「体積の求め方 円」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「体積の求め方 円」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「体積の求め方 円」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  |  |
「体積の求め方 円」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
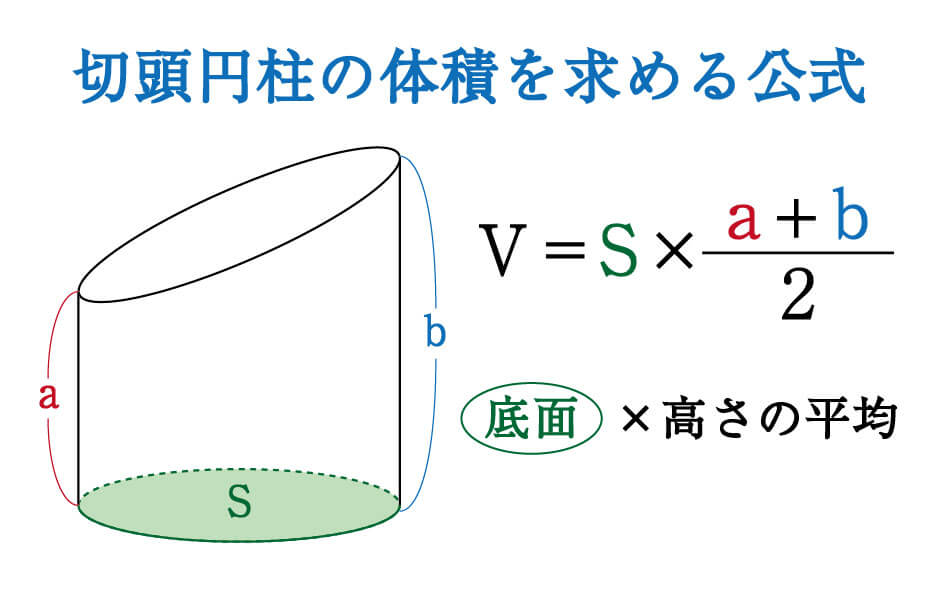 |
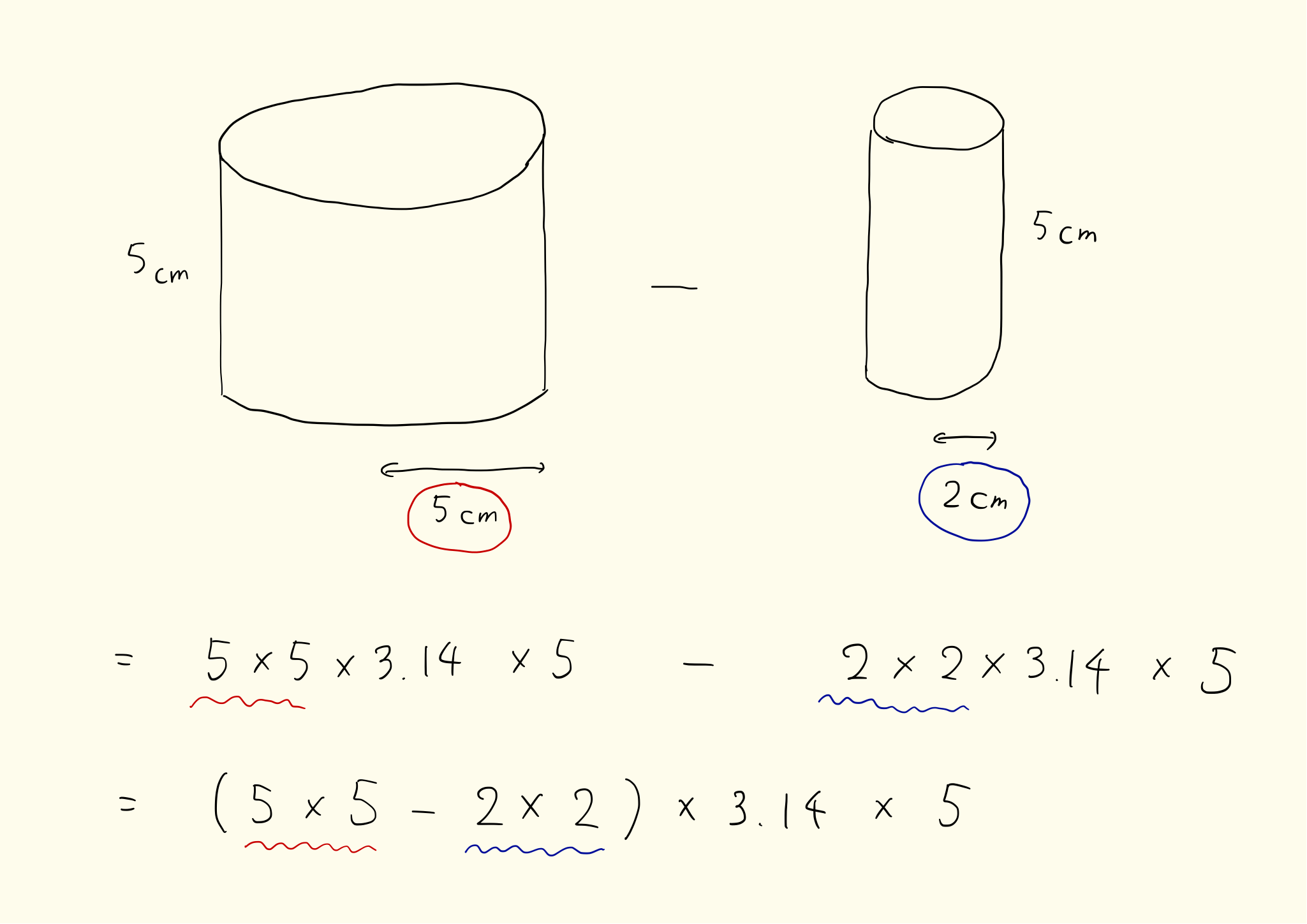
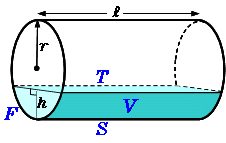
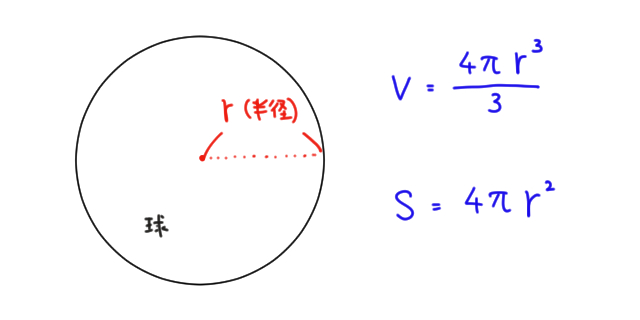
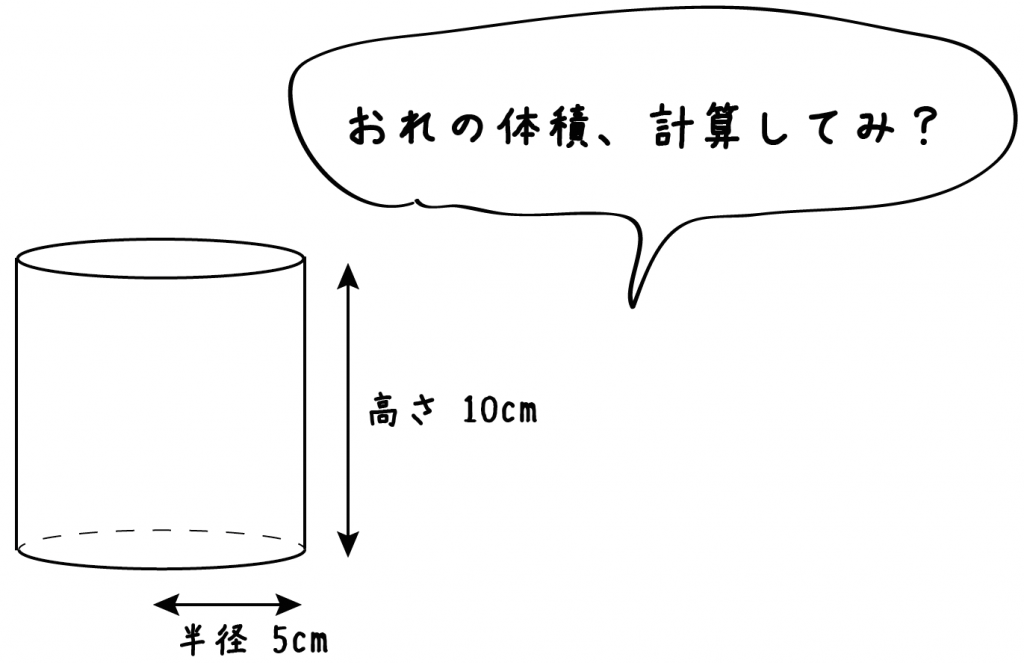
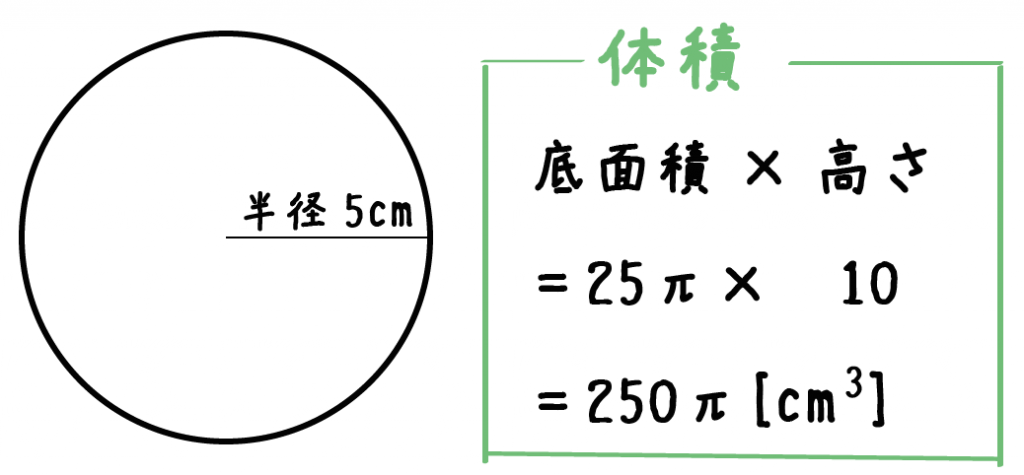
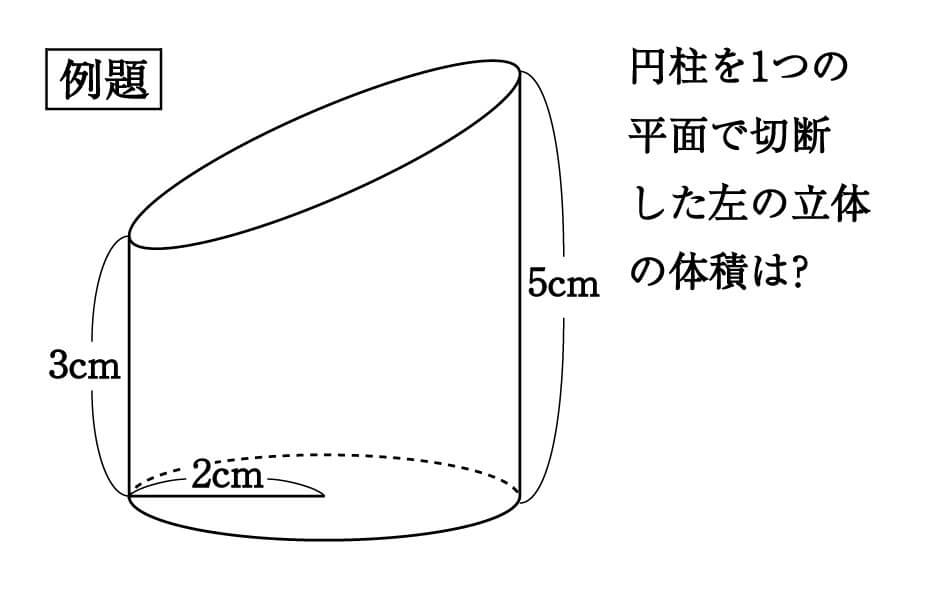
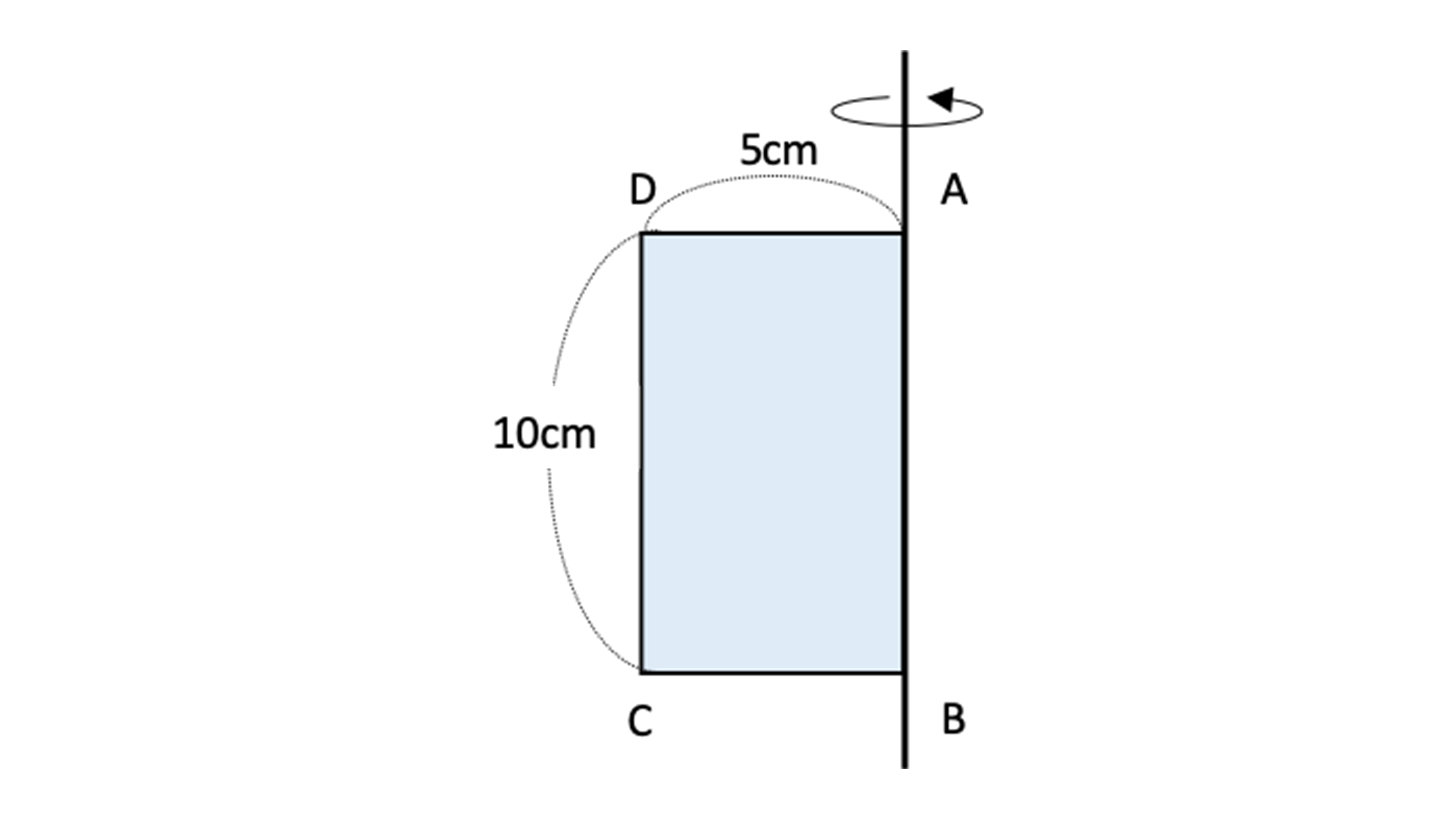
円錐の体積の求め方の公式って?? こんにちは、この記事をかいているKenだよ。犬の散歩が趣味だね。 円錐の体積の求め方の公式は、 底面積×高さ×1/3 だったよね。 もう少し詳しくかいてあげると、 半径×半径×円周率×円錐の高さ×1/3 になるんだ。 円柱の体積の求め方=半径×半径×円周率×高さ 円柱に関して、体積を求める問題がよく作られます。 たとえば上の写真のように、底の円の半径と円柱の高さが示されて「この円柱の体積を求めよ」と問われます。 上の情報を元に計算の流れを説明していきましょう。 まずは底面積 (S)を求めます。 「底面積=半径×半径×円周率」で計算できるので「6×6×π=36π
Incoming Term: 体積の求め方 円柱, 体積の求め方 円錐, 体積の求め方 円, 体積の求め方 円柱 リットル, 体積の求め方 円錐台,




0 件のコメント:
コメントを投稿